BCD o Código binario decimal es el sistema o código numérico que tiene los números o dígitos binarios para representar un número decimal.
Un número decimal contiene 10 dígitos (0-9). Ahora se pueden encontrar los números binarios equivalentes de estos 10 números decimales. En el caso de BCD el número binario formado por cuatro dígitos binarios, será el código equivalente para los dígitos decimales dados. En BCD podemos usar sólo el número binario de 0000-1001, que son el equivalente decimal de 0-9 respectivamente. Supongamos que si un número tiene un solo dígito decimal entonces su equivalente Código binario decimal serán los cuatro dígitos binarios respectivos de ese número decimal y si el número contiene dos dígitos decimales entonces su equivalente BCD será el respectivo ocho binario del número decimal dado. Cuatro para el primer dígito decimal y los siguientes cuatro para el segundo dígito decimal. Se puede borrar de un ejemplo.
Let, (12)10 será el número decimal cuyo equivalente Decimal con código binario será el 00010010. Cuatro bits de L.S.B. es el equivalente binario de 2 y los siguientes cuatro son el equivalente binario de 1.
En el cuadro que figura a continuación se muestran los BCD códigos para los números decimales del 0 al 15.
De la tabla siguiente, podemos concluir que después del 9 el número binario equivalente decimal es de cuatro bits, pero en el caso del BCD es un número de ocho bits. Esta es la principal diferencia entre el número binario y el decimal binario codificado. Para los números de 0 a 9 decimales tanto binario como BCD es igual, pero cuando el número decimal es de más de un bit BCD difiere del binario.
| Número decimal | Número binario | Decimal con código binario (BCD) |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0010 |
| 3 | 0011 | 0011 |
| 4 | 0100 | 0100 |
| 5 | 0101 | 0101 |
| 6 | 0110 | 0110 |
| 7 | 0111 | 0111 |
| 8 | 1000 | 1000 |
| 9 | 1001 | 1001 |
| 10 | 1010 | 0001 0000 |
| 11 | 1011 | 0001 0001 |
| 12 | 1100 | 0001 0010 |
| 13 | 1101 | 0001 0011 |
| 14 | 1110 | 0001 0100 |
| 15 | 1111 | 0001 0101 |
Adición de BCD
Al igual que otros sistemas de números en la operación aritmética del BCD puede ser necesario. BCD es un código numérico que tiene varias reglas de adición. A continuación se presentan las reglas en tres pasos con un ejemplo para hacer la idea de Adición de BCD despejado.
- Al principio, el número dado debe ser sumado usando la regla del binario. Por ejemplo,


- En el segundo paso tenemos que juzgar el resultado de la suma. Aquí se muestran dos casos para describir las reglas de Adición de BCD. En el caso 1 el resultado de la suma de dos números binarios es mayor que 9, lo cual no es válido para el número BCD. Pero el resultado de la suma en el caso 2 es menor que 9, lo cual es válido para los números BCD.
- Si el resultado de cuatro bits de la suma es mayor que 9 y si un bit de arrastre está presente en el resultado, entonces es inválido y tenemos que sumar 6 cuyo equivalente binario es (0110)2 al resultado de la suma. Entonces el resultado que obtendremos será un número codificado binario válido. En el caso 1 el resultado fue (1111)2que es mayor que 9, así que tenemos que añadir 6 o (0110)2 a ella.
Como pueden ver el resultado es válido en BCD.
Pero en el caso 2 el resultado ya era un BCD válido, así que no hay necesidad de sumar 6. Así es como podría ser la adición de BCD.
Ahora puede llegar la pregunta de por qué se añade el 6 al resultado de la suma en caso de la adición del BCD en lugar de cualquier otro número. Se hace para saltar los seis estados inválidos de decimal codificado binario, es decir, de 10 a 15 y volver de nuevo a los códigos BCD.
Ahora la idea de la adición de BCD puede ser aclarada de dos ejemplos más.
Ejemplo: 1
Let, 0101 se añade con 0110.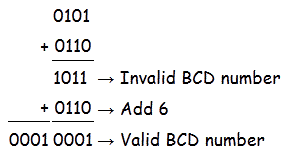

Revisa tu propio comportamiento.
Ejemplo: 2
Ahora dejemos que el 0001 0011 se añada al 0010 0110.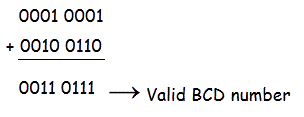
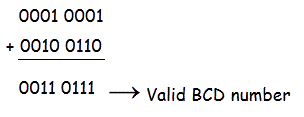
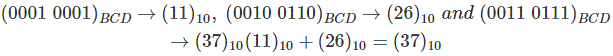
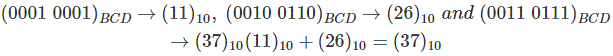
Así que no hay necesidad de añadir 6 porque ambos 
Sustracción de BCD
Hay varios métodos de Sustracción de BCD. La sustracción del BCD puede hacerse por el método de los complementos 1s y 9s o el método de los complementos 10s. Entre todos estos métodos, el método de los complementos 9s o el método de los complementos 10s es el más fácil. Aclararemos nuestra idea sobre los dos métodos de Sustracción de BCD.
Método de sustracción de BCD : 1
En el primer método haremos Sustracción de BCD por 1s elogio método. A continuación se muestran varios pasos para este método. Son:-
- Al principio se hace un cumplido del sustrato.
- Luego se añade la sustracción elogiada al otro número del que se va a hacer la sustracción. Esto se llama sumador 1.
- Ahora, en la sustracción de BCD hay un término EAC (end-around-carry). Si hay un carry, es decir, si EAC = 1 el resultado de la sustracción es +ve y si EAC = 0 entonces el resultado es ve. En la tabla que se muestra a continuación se indican las reglas de la EAC.
- En el resultado final, si se produce algún bit de arrastre, será ignorado.
| el transporte de grupos individuales | EAC = 1 | EAC = 0 |
| 1 | Transfiera el resultado real de la sumadora 1 y sume 0000 en la sumadora 2 | Transferencia 1s complemento resultado de la sumadora 1 y añadir 1010 en la sumadora 2 |
| 0 | Transfiera el resultado real de la sumadora 1 y sume 1010 en la sumadora 2 | Transfiera el resultado del complemento 1s de la sumadora 1 y añada 0000 a la sumadora 2 |
Los ejemplos que se dan a continuación aclararían la idea de la sustracción de BCD.
Ejemplo: 1
En este ejemplo 0010 0001 0110 se resta del 0101 0100 0001.
- Al principio se hace un complemento del sustrato, que es 1101 1110 1001 y se añade al 0101 0100 0001. Este paso se llama sumador 1.
- Ahora, después de la adición, si se produce cualquier arrastre, se añadirá al siguiente grupo de números hacia el MSB. Entonces se examinará el EAC. Aquí, EAC = 1. Así que el resultado de la suma es positivo y el verdadero resultado de la suma 1 se transferirá a la suma 2.
- Ahora un aviso de la LSB. Hay tres grupos de cuatro números de bits. 1010 se añade 1011 que es el primer grupo de números porque no tiene ninguna acarreo. El resultado de la suma es la respuesta final.
- La Carga 1 será ignorada tal y como es de la regla.
- Ahora pasa al siguiente grupo de números. 0000 se suma a 0010 y da el resultado 0010. Es el resultado final otra vez.
- Ahora de nuevo pasar al siguiente grupo aquí 0000 también se añade a 0011 para dar el resultado final 0011.
- Habrás notado que en estos dos grupos se agrega 0000, porque el resultado de la primera víbora no contiene ninguna carga. Por lo tanto, el resultado de la sumadora 2 es el resultado final de la Sustracción BCD.
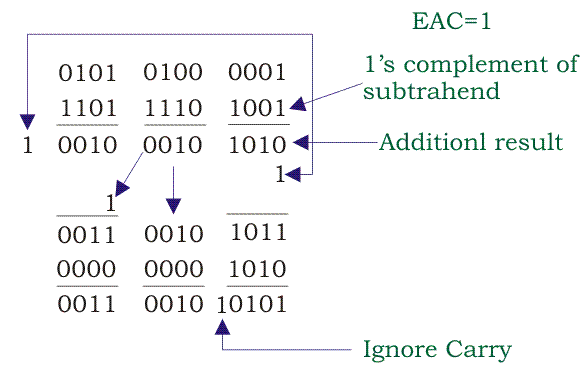

Por lo tanto,
Ahora puedes revisarte a ti mismo.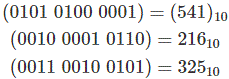
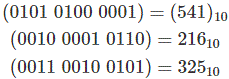
Sabemos que 541 216 = 325, por lo que podemos decir que nuestro resultado de Sustracción de BCD es correcto.
Ejemplo: 2
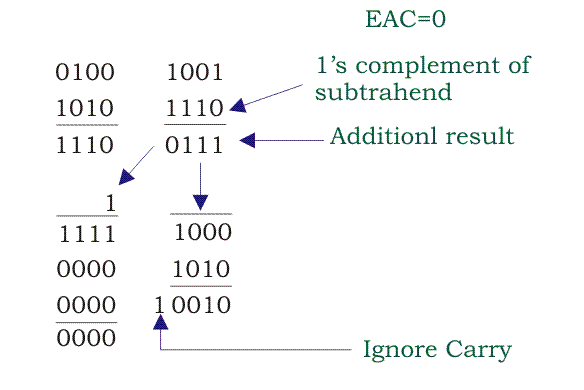
En este ejemplo, restemos 0101 0001 del 0100 1001.
- Por regla general, primero se hace un cumplido del sustrato. Luego se hace la suma y se comprueba el resultado. Aquí EAC = 0, por lo que el resultado global será ve.
- Ahora vea el resultado de la sumadora 1 de LSB. El valor de complemento 1s de 0111 se transfiere a la sumadora 2 y se añade con 1010 ya que no se añade ninguna acarreo con ella según la regla. La respuesta es el resultado final.
- Ahora pasa al siguiente resultado de la suma 1, es decir, 1110. Aquí se suma 1 que es el portador del resultado anterior. Entonces su valor es 1s complementado, es decir, 0000 y se suma a 0000. El resultado de la sumadora 2 es el resultado final. Este es el resultado final de la resta del BCD.
- Ahora puedes volver a revisarte. El equivalente decimal de los números dados de la resta es 49 y 51. Por lo tanto 49 -51 = -2. Así que nuestro resultado es correcto.

Método de sustracción de BCD: 2
En 2y haremos la sustracción de BCD en el método de complemento de 9s.
- Aquí el método es muy simple. Al principio se encuentra el equivalente decimal de los códigos decimales de código binario (BCD) dados.
- Luego se hace el complemento de 9s de la sustracción y luego ese resultado se suma al número del que se va a hacer la sustracción.
- Si hay algún bit de arrastre, entonces el bit de arrastre puede ser sumado al resultado de la resta.
La idea puede desprenderse de un ejemplo que se da a continuación.
Que (0101 0001) (0010 0001) sea la sustracción dada.
- Como podemos ver, 51 y 21 son el valor decimal de los códigos BCD dados. Entonces el complemento de 9s del sustraendo se hace, es decir, 99 21 = 78.
- Este valor complementario se añade con el 51. es decir, 51 + 78 = 129.
- En este resultado, el MSB, es decir, el 1, es el portador. Esta carga se sumará a 29. Por lo tanto 29 + 1 = 30, que es la respuesta final de Sustracción de BCD.
- El resultado decimal se cambiará a BCD códigos para obtener el resultado en BCD. Por lo tanto, a partir del ejemplo podemos concluir el resultado final de la Sustracción BCD, es decir


La resta decimal codificada binaria que utiliza el complemento de 10 es la misma que en el caso del complemento de 9, aquí la única diferencia es que en lugar del complemento de 9 tenemos que hacer el complemento de 10 de la resta.
Compresión BCD
Conversión de BCD es muy simple. En el caso de la conversión BCD, al principio el equivalente decimal de la BCD los códigos y luego ese número decimal puede cambiarse a cualquier otro sistema numérico según sea necesario. Para conocer los métodos de conversión del sistema numérico puede leer el tema sistema numérico binario.




