Carga de impedancia de sobretensión es un parámetro muy esencial cuando se trata del estudio de los sistemas de energía, ya que se utiliza en la predicción de la capacidad de carga máxima de líneas de transmisión.
Sin embargo, antes de entender SILprimero necesitamos tener una idea de lo que es Impedancia de la sobretensión (Zs). Se puede definir de dos maneras, una más simple y otra un poco más rigurosa.
Método 1
Es un hecho bien conocido que un largas líneas de transmisión (> 250 km) se han distribuido inductancia y capacitancia como su propiedad inherente. Cuando la línea se carga, el componente de capacitancia alimenta la línea con energía reactiva mientras que el componente de inductancia absorbe la energía reactiva. Ahora, si tomamos el balance de las dos potencias reactivas llegamos a la siguiente ecuación
VAR capacitivo = VAR inductivo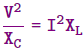
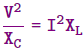
Dónde,
V = Voltaje de fase
I = Corriente de línea
Xc = Reactancia capacitiva por fase
XL = Reactancia inductiva por fase
Al simplificar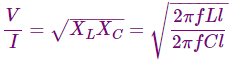
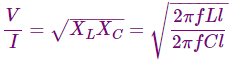
Dónde,
f = Frecuencia del sistema
L = Inductancia por unidad de longitud de la línea
l = Longitud de la línea
Por lo tanto, tenemos,![]()
![]()
Esta cantidad que tiene las dimensiones de resistencia es la Impedancia de la Oleada. Puede considerarse como una carga puramente resistiva que cuando se conecta en el extremo receptor de la línea, la potencia reactiva generada por la reactancia capacitiva será completamente absorbida por la reactancia inductiva de la línea.
No es nada más que la Impedancia Característica (Zc) de una línea sin pérdidas.
Método 2
De la rigurosa solución de un larga línea de transmisión obtenemos la siguiente ecuación para voltaje y actual en cualquier punto de la línea a una distancia x del extremo receptor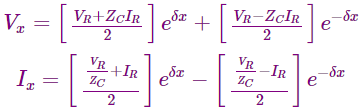
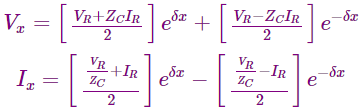
Dónde,
Vx y yox = Tensión y corriente en el punto x
VR y yoR = Tensión y corriente en el extremo receptor
Zc = Impedancia característica
= Constante de propagación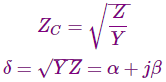
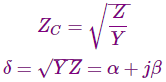
Z = Impedancia en serie por unidad de longitud por fase
Y = Admisión de la derivación por unidad de longitud por fase
Poniendo el valor de en encima de la ecuación de voltaje obtenemos![]()
![]()
Dónde,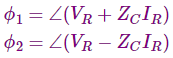
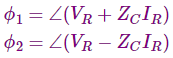
Observamos que el voltaje instantáneo consiste en dos términos, cada uno de los cuales es una función del tiempo y la distancia. Por lo tanto, representan dos ondas viajeras. La primera es la parte exponencial positiva que representa una onda que viaja hacia el extremo receptor y por lo tanto se llama la onda incidente. Mientras que la otra parte con exponencial negativa representa la onda reflejada. En cualquier punto a lo largo de la línea, el voltaje es la suma de ambas ondas. Lo mismo ocurre con las ondas de corriente también.
Ahora, si suponemos que la impedancia de la carga (ZL) es elegido de tal manera que ZL = Zcy sabemos que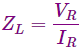
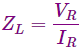
Así,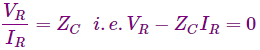
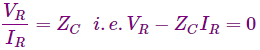
y por lo tanto la onda reflejada se desvanece. Tal línea se denomina línea infinita. A la fuente le parece que la línea no tiene fin porque no recibe ninguna onda reflejada.
Por lo tanto, tal impedancia que hace que la línea sea infinita se conoce como impedancia de sobretensión. Tiene un valor de unos 400 ohmios y un ángulo de fase que varía de 0 a 15 grados para las líneas aéreas y alrededor de 40 ohmios para los cables subterráneos.
Sin embargo, el término impedancia de sobretensión se utiliza en relación con las sobretensiones en la línea de transmisión que puede ser debido a un rayo o a una conmutación, donde las pérdidas de la línea pueden ser descuidadas de tal manera que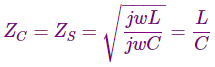
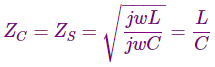
Ahora que hemos entendido la Impedancia de Onda, podemos definir fácilmente Carga de impedancia de sobretensión.
SIL se define como la potencia suministrada por una línea a una carga puramente resistiva de valor igual a la impedancia de la línea. Por lo tanto, podemos escribir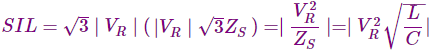
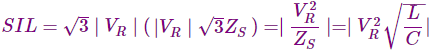
La unidad del SIL es Watt o MW.
Cuando la línea termina por una impedancia de sobretensión, el voltaje del extremo receptor es igual al voltaje del extremo emisor y este caso se llama perfil de voltaje plano. La siguiente figura muestra el perfil de voltaje para diferentes casos de carga.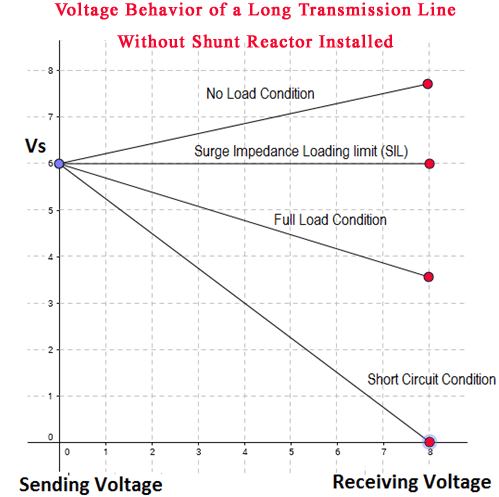

Cabe señalar también que la impedancia de la oleada y, por lo tanto, el SIL es independiente de la longitud de la línea. El valor de la impedancia de sobretensión será el mismo en todos los puntos de la línea y por lo tanto el voltaje.
En el caso de una línea compensada, el valor de la impedancia de la oleada se modificará en consecuencia como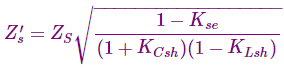
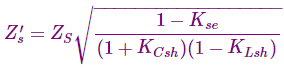
¿Dónde, Kse = % de compensación capacitiva en serie por Cse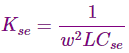
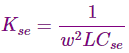
KCsh = % de compensación capacitiva de la derivación por Csh![]()
![]()
Klsh = % de compensación inductiva de la derivación por Lsh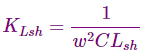
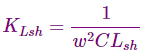
La ecuación para SIL utilizará ahora la Z modificadas.