Una señal, comprende un conjunto de información expresada en función de cualquier número de variables independientes, que puede darse como entrada a un sistema, o derivarse como salida del sistema, para realizar su verdadera utilidad práctica. La señal que obtenemos de un sistema complejo puede no siempre ser de la forma que queremos,
estar bien familiarizado con algunos operaciones básicas de señales puede ser muy útil para mejorar la comprensión y la aplicabilidad de las señales.
La transformación matemática de una señal a otra puede expresarse como
Donde, Y(t) representa la señal modificada derivada de la señal original X(t), teniendo sólo una variable independiente t.
El conjunto básico de operaciones de señales pueden clasificarse a grandes rasgos como sigue.
Operaciones básicas de señales realizadas con variables dependientes
En esta transformación, sólo se modifican los valores del eje de cuadratura, es decir, cambia la magnitud de la señal, sin efectos sobre los valores del eje horizontal o la periodicidad de las señales como.
- Escalado de amplitud de las señales.
- Adición de señales.
- Multiplicación de señales.
- Diferenciación de señales.
- Integración de señales.
Veamos estos tipos en detalle.
Escalado de amplitud de las señales
El escalado de la amplitud es una operación muy básica que se realiza en las señales para variar su fuerza. Se puede representar matemáticamente como Y(t) = α X(t).
Aquí, α es el factor de escala, donde:-
<1 señal es atenuada. >1 señal es amplificada.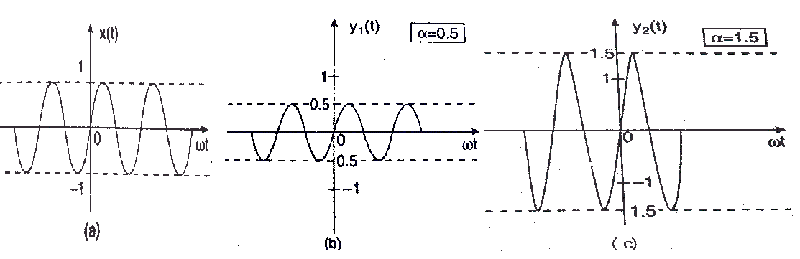

Esto se ilustra en el diagrama, donde la señal es atenuada cuando = 0,5 en la figura (b) y amplificada cuando = 1,5 como en la figura (c).
Adición de señales
Esta operación particular implica la adición de la amplitud de dos o más señales en cada instancia de tiempo o cualquier otra variable independiente que sea común entre las señales. La adición de señales se ilustra en el siguiente diagrama, donde X1(t) y X2(t) son dos señales dependientes del tiempo, realizando la operación adicional que obtenemos de ellas,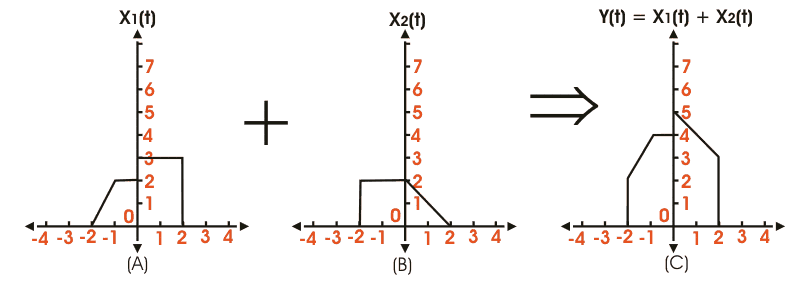
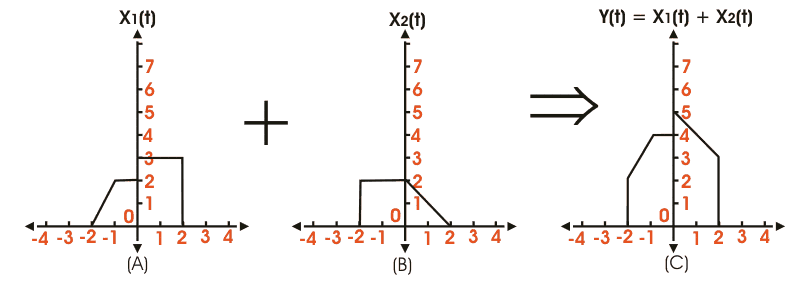
Multiplicación de señales
Al igual que la suma, la multiplicación de señales también entra en la categoría de operaciones básicas de señales. Aquí se hace la multiplicación de la amplitud de dos o más señales en cada instancia de tiempo o cualquier otra variable independiente que sea común entre las señales. La señal resultante que obtenemos tiene valores iguales al producto de la amplitud de las señales parentales para cada instancia de tiempo. La multiplicación de las señales se ilustra en el siguiente diagrama, donde X1(t) y X2(t) son dos señales dependientes del tiempo, de las que después de realizar la operación de multiplicación obtenemos,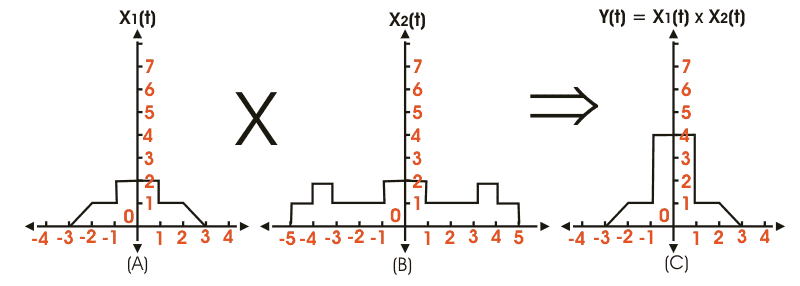

Diferenciación de las señales
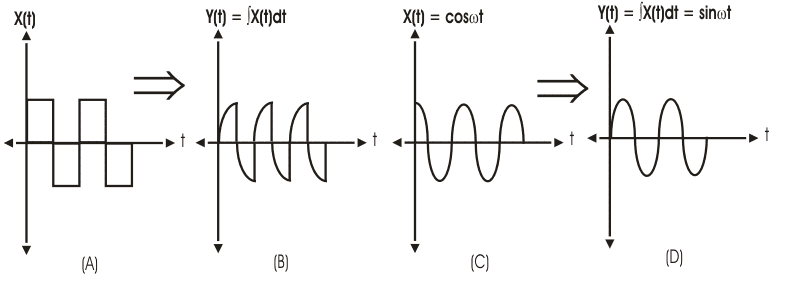

Para la diferenciación de las señales, hay que señalar que esta operación sólo es aplicable para las señales continuas, ya que no se puede diferenciar una función discreta. La señal modificada que obtenemos en la diferenciación tiene valores tangenciales de la señal madre en todo momento. Matemáticamente se puede expresar como:-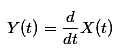
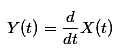
La diferenciación de una onda cuadrada estándar y una onda sinusoidal se muestra en la siguiente figura.
Integración de las señales
Al igual que la diferenciación, la integración de las señales también es aplicable sólo a las señales de tiempo continuo. Los límites de la integración serán desde el momento presente del tiempo t. Se expresa matemáticamente como,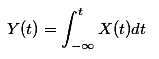
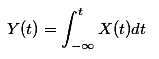
La integración de algunas señales temporales continuas se muestra en el diagrama siguiente.

Operaciones básicas de señales realizadas con variables dependientes
Esto es exactamente lo contrario del caso anterior, aquí la periodicidad de la señal se varía modificando los valores del eje horizontal, mientras que la amplitud o la fuerza permanece constante. Estos son:-
- Escalado temporal de las señales
- Reflexión de las señales
- Cambio de tiempo de las señales.
Veamos estas operaciones en detalle.
Escala de tiempo de las señales
La escalada temporal de las señales de las señales implica la modificación de una periodicidad de la señal, manteniendo su amplitud constante. Se expresa matemáticamente como,
Donde, X(t) es la señal original, y es el factor de escala.
Si > 1 implica, la señal se comprime y < 1 implica, la señal se expande. Esto se ilustra en forma de diagrama para una mejor comprensión.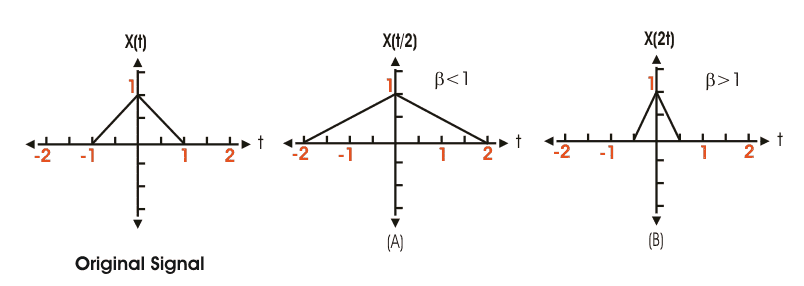

Reflexión de las señales
La reflexión de la señal es una operación muy interesante aplicable tanto a las señales continuas como a las discretas. Aquí en este caso el eje vertical actúa como el espejo, y la imagen transformada que se obtiene es exactamente la imagen espejo de la señal madre.
Se puede definir como Y(t) = X(- t) donde, X(t) es la señal original.
Pero si la señal reflejada X(- t) = X(t); entonces se llama señal par.
Donde cuando X(- t) = X(t); entonces se conoce como una señal extraña.
Se explica diagramáticamente como,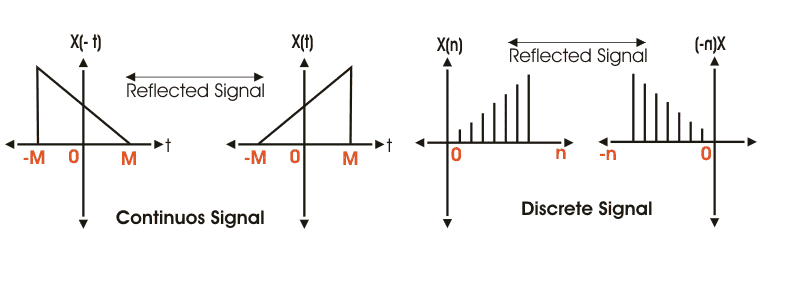

Cambio de tiempo de las señales
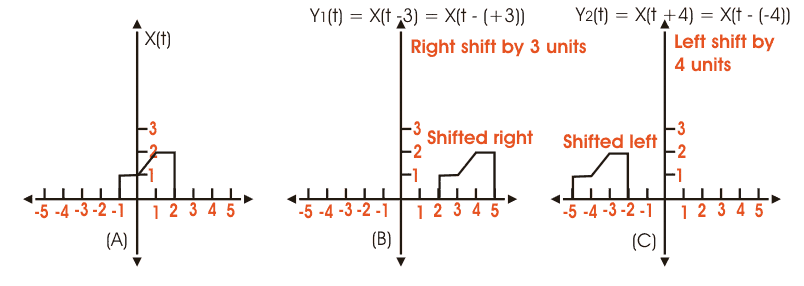
El desplazamiento temporal de las señales es probablemente el más importante, y el más utilizado entre todos operaciones básicas de señales. Se utiliza generalmente para adelantar o retrasar una señal, como es necesario en la mayoría de las circunstancias prácticas. El cambio de tiempo se expresa matemáticamente como,
Donde, X(t) es la señal original, y t0 representa el cambio en el tiempo.
Para una señal X(t) si el cambio de posición t0> 0. Entonces se dice que la señal está bien desplazada o retrasada.
De la misma manera, si0 < 0, implica que la señal se deja desplazada o retrasada. Esto se ha explicado esquemáticamente en la siguiente figura. Donde la señal original fig(a) está desplazada a la derecha y también a la izquierda en las figuras (b) y (c) respectivamente.