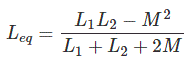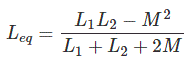Cuando los inductores están conectados en serie la inductancia equivalente de la combinación será la simple suma de la inductancia de todos los inductores individuales. Esto es como el equivalente resistencia de resistencias conectadas en serie. Pero en el caso de inductoresa veces tenemos que considerar el efecto de inducción mutua entre el inductores. Entonces el para el cálculo de la inductancia de cada inductor que consideramos tanto el autoinducción y inducción mutua del inductor. El inducción mutua se añadirá o se restará de la autoinducción dependiendo de la polaridad de los inductores acoplados magnéticamente. Aprenderemos sobre el efecto de la inductancia mutua más adelante en este artículo. Ahora, sin considerar las inductancias mutuas podemos escribir la inductancia equivalente de los inductores conectados en serie como,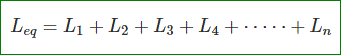
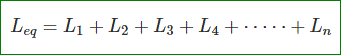
Cuando los inductores están conectados en paralelo el recíproco de la inductancia equivalente de la combinación será la suma del recíproco de las inductancias individuales. Esto es igual que el equivalente resistencia de resistencias conectadas en paralelo. Aquí también podemos tener que considerar el efecto de la inducción mutua de la misma manera si es necesario. Aprenderemos el efecto de la inductancia mutua en los inductores paralelos más adelante en este artículo. Sin considerar el efecto de la inductancia mutua podemos escribir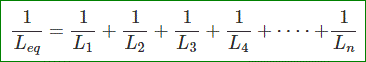
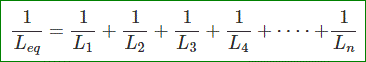
Un inductor es un elemento de circuito pasivo. Averigüemos la inductancia equivalente de inductores conectados en serie y en paralelo.
Inductores conectados en serie
Consideremos n número de inductores conectados en serie como se muestra a continuación.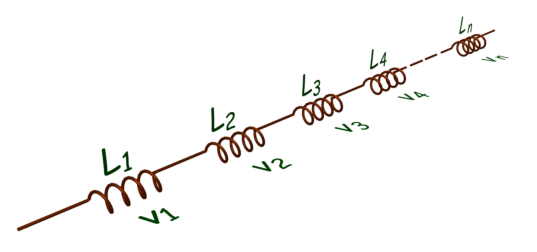

Consideremos también eso,
el inductancia del inductor 1 y Caída de tensión a través de ella están L1 y v1 En realidad..,
la inductancia del inductor 1 y la caída de voltaje a través de él son L2 y v2 En realidad..,
la inductancia del inductor 1 y la caída de voltaje a través de él son L3 y v3 En realidad..,
la inductancia del inductor 1 y la caída de voltaje a través de él son L4 y v4 En realidad..,
el inductancia del inductor 1 y la caída de voltaje a través de él son Ln y vn En realidad…
Ahora, aplicando, Ley de tensión de Kirchhoffs…tenemos, total… voltaje gota a gota (v) a través de la combinación en serie de los inductores,
La caída de voltaje a través de un inductor de inductancia L puede expresarse como,![]()
![]()
Donde, es la instantánea actual a través del inductor.
Como todos los inductores de las combinaciones están conectados en serie, aquí, la corriente a través de cada uno de los inductores es la misma, y digamos que también es i. Así que, desde arriba KVL ecuación, tenemos,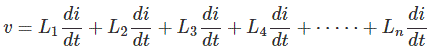
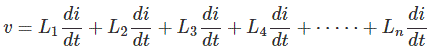
Esta ecuación puede ser reescrita como,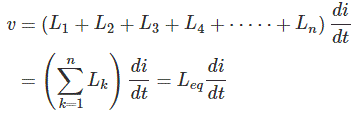
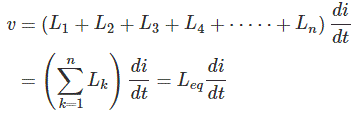
¿Dónde, Leq es la inducción equivalente de la inductores combinados en serie. Por lo tanto,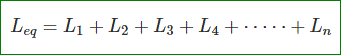
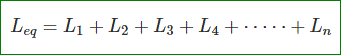
La inductancia equivalente de los inductores conectados en serie es simplemente la suma aritmética de la inductancia de los inductores individuales.
Inductores conectados en paralelo
Consideremos n número de inductores conectados en paralelo como se muestra a continuación.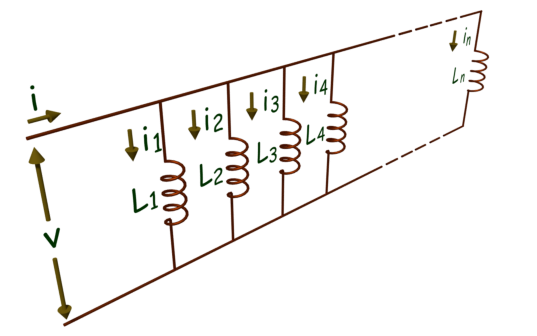

Consideremos también eso,
el inductancia del inductor 1 y la corriente que lo atraviesa son L1 y yo1 En realidad..,
la inductancia del inductor 1 y la corriente que lo atraviesa son L2 y yo2 En realidad..,
la inductancia del inductor 1 y la corriente que lo atraviesa son L3 y yo3 En realidad..,
la inductancia del inductor 1 y la corriente que lo atraviesa son L4 y yo4 En realidad..,
la inductancia del inductor 1 y la corriente que lo atraviesa son Ln y yon En realidad…
Ahora, aplicando, Ley actual de Kirchhoffsobtenemos, la corriente total (i) entrando en el combinación paralela de los inductores,![]()
![]()
La corriente a través de un inductor de inductancia L puede expresarse como,
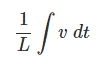
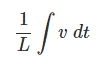
Donde, v es el voltaje instantáneo a través del inductor.
Como todos los inductores de las combinaciones están conectados en paralelo, aquí, el Caída de tensión a través de cada uno de los inductores es el mismo, y digamos también que es v. Así que, desde arriba KCL ecuación, tenemos,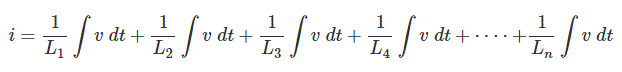
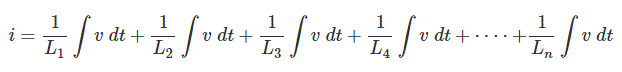
Esta ecuación puede ser reescrita como,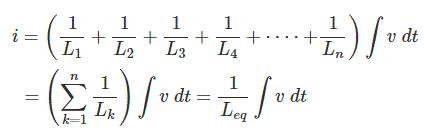
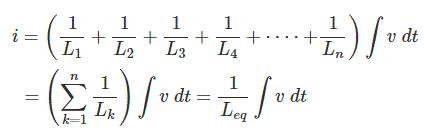
¿Dónde, Leq es la inducción equivalente de la inductores combinados en paralelo. Por lo tanto,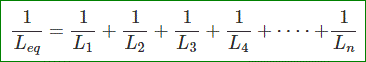
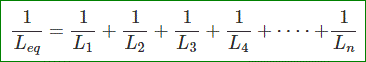
El recíproco de la inductancia equivalente de los inductores de conexión paralela es simplemente la suma aritmética del recíproco de la inductancia de los inductores individuales.
Efecto de la inducción mutua en los inductores conectados en serie
Cuando más de un inductor se acerca, puede haber una inducción mutua entre ellos. Si más de un inductor está conectado en serie y el flujo de un inductor enlaza al otro, entonces tenemos que considerar la inductancia mutua durante los cálculos de la inductancia equivalente. Para este propósito, utilizamos la convención de los puntos. Aquí cada uno de los inductores está marcado con un punto en un extremo. La corriente que entra por el terminal punteado de un inductor inducirá un voltaje en el otro inductor con polaridad positiva en el terminal punteado de este último. Consideremos el siguiente ejemplo.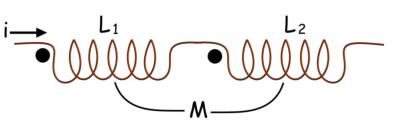

Como los inductores están en serie, la misma corriente fluirá a estos inductores. Por lo tanto, cuando la corriente entra a través del terminal de puntos del inductor 1, la corriente entra a través del terminal de puntos del inductor 2. El inductor 2 inducirá el voltaje a través del inductor 1 con polaridad positiva en el terminal punteado del inductor 1. La corriente entra por el terminal punteado del inductor 1 inducirá el voltaje a través del inductor 2 con polaridad positiva en el extremo punteado del inductor 2. Como las dos EMF mutuamente inducidas están en la dirección EMF autoinducida las impedancias equivalentes, la inductancia mutua simplemente se sumará a la autoinducción para calcular la impedancia equivalente.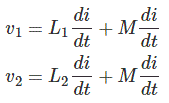
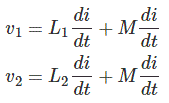
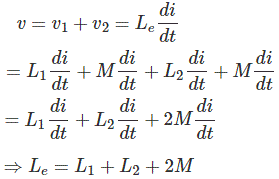
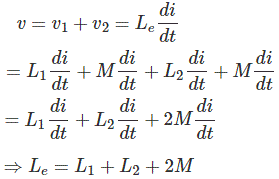
Aquí, en este segundo ejemplo, según la convención de puntos que se presenta en la figura siguiente, la corriente está entrando por el terminal de puntos de un inductor y la misma corriente está saliendo del terminal de puntos del otro inductor. En ese caso la polaridad de la emf mutuamente inducida difiere de la emf autoinducida. La inductancia equivalente de la combinación será 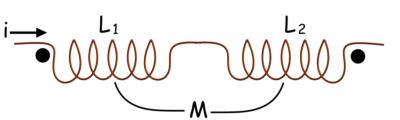

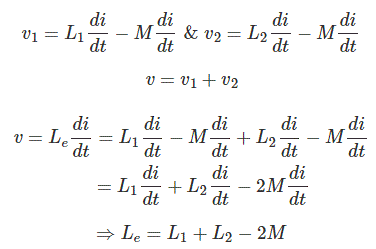
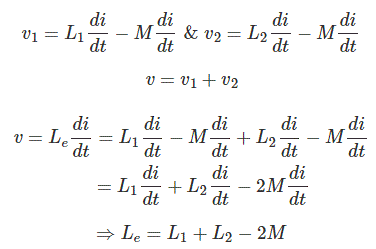
Efecto de la inducción mutua en los inductores conectados en paralelo
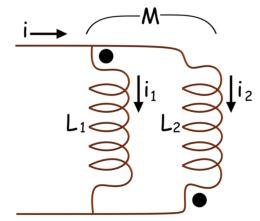
Ahora llegaremos al efecto de la inductancia mutua en los inductores conectados en paralelo. Aquí en este ejemplo se dan puntos al mismo lado de dos inductores. Cuando la corriente entra a través del terminal punteado del inductor 1, el EMF inducido tiene la polaridad positiva en el extremo punteado del inductor 2. 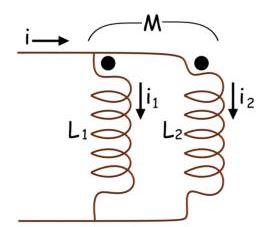

De manera similar, cuando la corriente entra por el terminal punteado del inductor 2, la EMF inducida en el inductor 1 tiene una polaridad positiva en el extremo punteado del inductor 1. Así que la inductancia equivalente es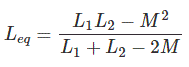
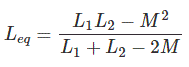
Del mismo modo, cuando dos inductores paralelos se puntean de la siguiente manera, la inductancia equivalente será