¿Qué es la ecuación de Schrodinger
El Ecuación de Schrdinger (también conocido como Ecuación de onda de Schrdingers) es una ecuación diferencial parcial que describe la dinámica de los sistemas mecánicos cuánticos a través de la función de onda. La trayectoria, el posicionamiento y la energía de estos sistemas pueden recuperarse resolviendo la ecuación de Schrdinger.
Toda la información de una partícula subatómica está codificada dentro de una función de onda. La función de onda satisfará y puede ser resuelta usando la ecuación de Schrodinger. La ecuación es uno de los axiomas fundamentales que se introducen en la física de grado. También es cada vez más común encontrar que la ecuación de Schrdinger se introduce en el programa de estudios de ingeniería eléctrica en las universidades, ya que es aplicable con semiconductores.
Lamentablemente, sólo se afirma como un postulado en ambos casos y nunca se deriva de manera significativa. Esto es bastante insatisfactorio ya que casi todo lo demás que se enseña en la licenciatura de física cuántica se construye sobre esta base. En este artículo, derivaremos la ecuación desde cero y haré todo lo posible para mostrar cada paso dado. Curiosamente, los argumentos que presentaremos son los mismos que los del propio Schrdinger para que puedan ver las líneas de pensamiento que un gigante estaba haciendo en su tiempo. Como recordatorio, aquí está la ecuación de Schrdinger dependiente del tiempo en 3 dimensiones (para una partícula no relativista) en toda su belleza:
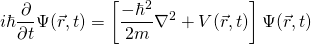
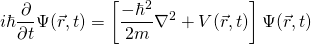
Física Cuántica y Ondas
A todo el mundo le gusta embolsarse la física clásica, pero nos sirvió bastante bien durante un tiempo (pensemos en la mecánica newtoniana, las ecuaciones de Maxwells y la relatividad especial). Sin embargo, como se muestra en nuestros artículos anteriores, los resultados experimentales de principios de siglo no parecían demasiado brillantes en comparación con la física conocida en ese momento. Nuestros artículos sobre la experimento de doble rendija y hasta cierto punto el efecto fotoeléctrico son resultados experimentales que no coinciden con la comprensión conocida de la época. ¿Pero por qué? Para decirlo de forma simple, en la física clásica existen dos entidades, las partículas y olas. Las características de ambas entidades pueden describirse como sigue:
- Partículas: haces de energía e impulso localizados con masa
.
- Ondas: perturbaciones que se extienden por el espacio viajando en el tiempo. Se pueden describir con una función de onda
que describe la onda sobre el espacio y el tiempo.
Esto nos lleva a los sorprendentes resultados encontrados en nuestra Emisión fotoeléctrica artículo. Encontramos que el electrón muestra ambos de estas propiedades. Esto estaba en completa contradicción con el entendimiento conocido de la época ya que las dos entidades se consideraban mutuamente excluyentes. Una locura, ¿verdad? En esta época, algunas figuras realmente influyentes en la física comenzaron a darse cuenta de que había una brecha en el conocimiento, y un gran avance se produjo cuando Louis de Broglie asoció un impulso (para una partícula) a una longitud de onda (para las ondas) dada por
Además, desde Emisión fotoeléctrica sabemos que allí la absorción de energía y la emisión de fotones (aún no se sabe si es una partícula u onda) tienen la energía dada por:
Donde 
y 
. Estamos ahora en la misma etapa en la que Schrdinger estaba antes de derivar su famosa ecuación. Pero, ¿por dónde empezamos? Bueno, sabemos que los electrones y los fotones muestran un comportamiento ondulatorio y de partículas. No habría nada de malo en comenzar con una ecuación universal que todas las ondas deben obedecer y luego introducir la física de partículas en la parte superior para ver si hay un resultado.
Cómo derivar la ecuación de la onda
La perturbación obedece a la ecuación de la onda. Recuerde, el electrón muestra un comportamiento ondulatorio y tiene una carga electromagnética. Por lo tanto, por ahora, veamos los campos electromagnéticos. En este escenario, se aplican las ecuaciones de Maxwell y aquí están en toda su gloria:
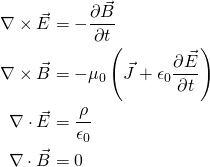
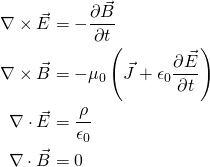
Donde 
es la velocidad de la luz en el vacío, 
es el campo eléctrico y 
es el campo magnético. La primera ecuación anterior es la base de los generadores eléctricos, inductores y transformadores y es la encarnación de la Ley de Faraday. Además, una de las implicaciones de 
es que no existen monopolos magnéticos. Entender la derivación de estas ecuaciones y el significado físico que hay detrás de ellas hace que sea un ingeniero muy completo. Ahora, derivemos la ecuación que cualquier onda electromagnética debe obedecer aplicando un rizo a la Ecuación 4:
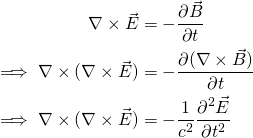
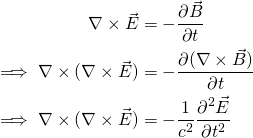
Ahora podemos aprovechar una identidad vectorial muy familiar (y fácilmente demostrable): 
donde 
es un vector de marcador de posición. Aplicando a nuestra pequeña ecuación ahora:
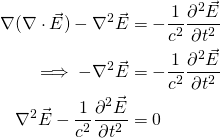
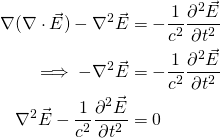
El resultado que tenemos aquí es la ecuación de la onda electromagnética en 3 dimensiones. Esta ecuación no sólo se manifiesta en una onda electromagnética, sino que también se ha mostrado en la acústica, las ondas sísmicas, las ondas de sonido, las ondas de agua y la dinámica de fluidos.
Cómo derivar la ecuación de Schrdinger
Soluciones de ondas planas a la ecuación de la onda
Comenzando con la ecuación de onda para 1 dimensión (es realmente fácil generalizar a 3 dimensiones después, ya que la lógica se aplicará en todas 
y 
dimensiones.):
Esta es en realidad una ecuación diferencial parcial de segundo orden y se satisface con soluciones de ondas planas:
Donde sabemos por la mecánica de ondas normales que 
y 
. Ahora, hagamos uso del trabajo de Einstein y Compton y substituyamos el hecho de que la energía de un fotón es dada por 
y de de-Broglie que 
. Podemos masajear aún más nuestra solución de ondas planas:
Esta es la ecuación de onda plana que describe un fotón. Sustituyamos esta ecuación por nuestra ecuación de onda y veamos qué encontramos.
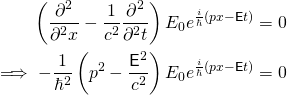
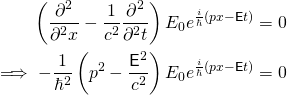
En otras palabras, 
lo cual es genial porque sabemos por la relatividad especial que la energía total para una partícula relativista con masa 
es:
y hasta ahora sólo hemos tratado con el fotón que no tiene masa 
! Así que ampliemos nuestra comprensión y apliquemos la energía relativista total para una partícula con masa (como el electrón por ejemplo) y cambiemos el nombre de nuestra ecuación a 
porque eran ballers.
Esta ecuación vino directamente de la sustitución de la ecuación de onda plana por un fotón en la ecuación de onda. Sin embargo, como ahora queremos que la energía resuelva la energía relativista total para una partícula con masa, necesitamos cambiar ligeramente la ecuación de onda. Esto se debe a que la ecuación de onda no debería aplicarse completamente a nuestro nuevo 
que describe las partículas y las ondas. Ahora podemos retroceder para que un operador obtenga la ecuación anterior, y que ésta sea dada por:
Resolver para las partículas con masa en la ecuación de la onda
Ahora queremos hacer algunas aproximaciones sobre la energía total que acabamos de describir 
para una partícula con impulso y masa. Reorganicemos la fórmula ligeramente para poder usar algunas aproximaciones.
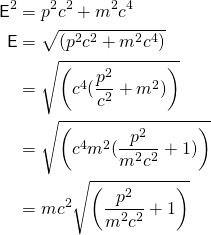
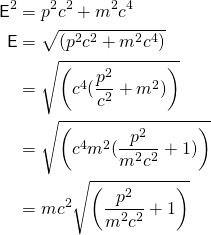
El objetivo de esta manipulación es obtener la ecuación en la forma 
porque si tomamos una expansión de la Serie Taylor de esta ecuación obtenemos:
Cuando 
es pequeña, la única parte que queda en la expansión de Taylor es la 
término. En nuestra fórmula de energía, 
. Podemos aprovechar el hecho de que 
para cualquier cosa que no viaje a la velocidad de la luz (por favor, encuéntreme si encuentra algo que no satisfaga esto)! Así que este término se reduce a:
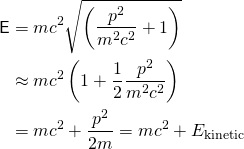
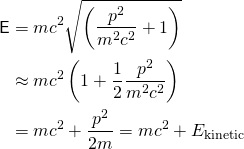
Donde
es la energía cinética normal que vemos en la física de la escuela secundaria. Ahora volvamos a la función de onda de antes, introduzcamos esta nueva información y veamos con qué terminamos:
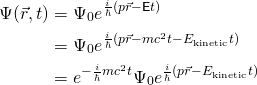
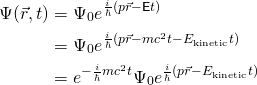
La razón por la que hemos dividido los dos términos es que el primer término 
(sólo basado nuevamente en la velocidad de la luz) será significativamente más oscilatorio que el del segundo término y no describe necesariamente la entidad de onda-partícula que buscamos. Así que para solidificar esta diferencia, establezcamos ahora eso:
Donde hemos definido ahora:
Tomemos ahora la primera y segunda derivadas parciales de 
y ver con qué terminamos. El primero:
y el segundo:
Debemos tener en cuenta que el último término con la segunda derivada parcial es bastante pequeño debido al hecho de que no hay 
término que lleva el orden de magnitud, y por lo tanto por aproximación la segunda derivada real viene dada por
La astuta razón por la que tomamos estas dos derivadas parciales fue para poder imputarlas en esta ecuación que describe la función de onda anteriormente:
Pero antes de que podamos hacer eso, reordenemos esta fórmula y terminemos con una ecuación llamada la ecuación de Klein-Gordon:
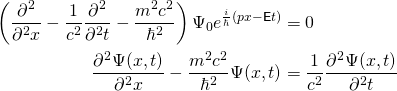
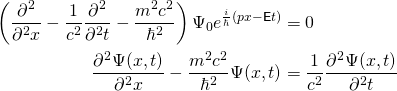
Ahora podemos fácilmente generalizar esto a 3 dimensiones convirtiendo esta ecuación en una ecuación vectorial (todos los pasos que dimos para derivar esta fórmula se aplicarán para todos los 
y .)
Esta ecuación se conoce como la ecuación de Klein-Gordon para un partículo libre. Esta ecuación es relativista ya que su término de energía no hace suposiciones que hicimos con el pequeño 
La expansión de Taylor. Ahora, simplifiquemos la ecuación de Klein-Gordon (bajando a 1-D y aplicando nuestra nueva fórmula de energía) y lleguemos bien a la tan esperada Ecuación de Schrdinger:
Pongamos en nuestra nueva función de onda dada por 
donde sabemos cómo son la primera y la segunda derivadas con respecto al tiempo:
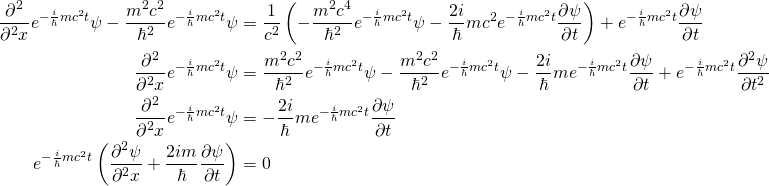
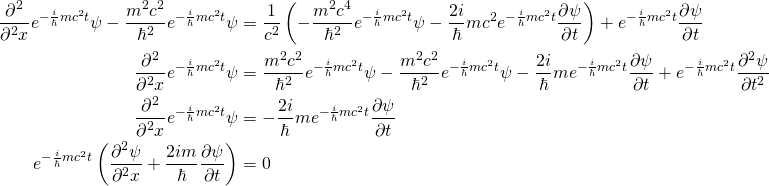
Ahora todo lo que necesitamos hacer es un simple reordenamiento para obtener la Ecuación de Schrdinger en tres dimensiones (note que 
):
Donde el argumento puede hacerse notar la similitud del clásico Hamiltoniano de que el término en el lado derecho de la ecuación describe la energía total de la función de onda. En nuestra derivación, asumimos que 
es 0 y que sólo se tuvo en cuenta la energía cinética. Sabemos que el potencial es puramente aditivo con respecto a sus variaciones espaciales y por lo tanto, la ecuación de Schrdinger completa en tres dimensiones con un potencial está dada por:
¡Eso es! Ahí lo tenemos, este artículo ha deducido la ecuación completa de Schrodinger para una partícula no relativista en tres dimensiones. Si te ha gustado este post y te gustaría ver más como esto, por favor envíanos un correo electrónico para hacérnoslo saber.
Citas
- Gasiorowicz, S. (2019). Física cuántica. 2ª edición. Canadá: Hamilton Printing, pp.1-50.
- Griffiths, D. (2019). Física cuántica. 3ª ed. University Printing House, Cambridge: Cambridge University Press.
- Ward, D. y Volkmer, S. (2019). Cómo derivar la ecuación de Schrodinger. [en línea] arXiv.org. Disponible en: https://arxiv.org/abs/physics/0610121v1 [Accedido el 29 de mayo de 2019].
- Shankar, R. (1980).Principios de la mecánica cuántica. 1a edición. Nueva York: Springer Science, pp.1-40.
