En Circuito RLClos elementos más fundamentales como resistencia, inductor y condensador están conectados a través de un voltaje suministro. Todos estos elementos son de naturaleza lineal y pasiva, es decir, consumen energía en lugar de producirla y estos elementos tienen una relación lineal entre el voltaje y actual. Hay varias maneras de conectar estos elementos a través de la alimentación de voltaje, pero el método más común es conectar estos elementos en serie o en paralelo. El Circuito RLC exhibe la propiedad de resonancia de la misma manera que el circuito LC, pero en este circuito la oscilación se extingue rápidamente en comparación con el circuito LC debido a la presencia de una resistencia en el circuito.
Circuito RLC en serie
Cuando una resistencia, un inductor y un condensador se conectan en serie con el suministro de voltaje, el circuito así formado se llama circuito RLC en serie.
Como todos estos componentes están conectados en serie, la corriente en cada elemento sigue siendo la misma,

Que VR …es el voltaje a través de la resistencia, R.
VL …es el voltaje a través del inductor, L.
VC …es el voltaje a través del condensador, C.
XL ser la reactancia inductiva.
XC ser la reactancia capacitiva.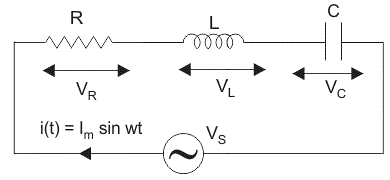

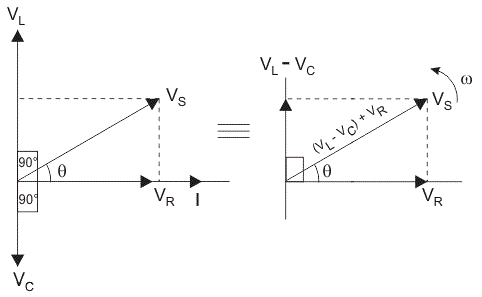
El voltaje total en el circuito RLC no es igual a la suma algebraica de los voltajes a través de la resistencia, el inductor y el condensador; pero es una suma vectorial porque, en el caso de la resistencia el voltaje está en fase con la corriente, para el inductor el voltaje lleva a la corriente en un 90o y para el condensador, el voltaje se retrasa con respecto a la corriente en un 90o. Así que los voltajes de cada componente no están en fase con cada uno de los otros, por lo que no se pueden sumar aritméticamente. La siguiente figura muestra el diagrama de fases del circuito RLC en serie. Para dibujar el diagrama de fases del circuito en serie RLC, se toma como referencia la corriente porque, en el circuito en serie, la corriente en cada elemento permanece igual y los correspondientes vectores de tensión para cada componente se dibujan en referencia al vector de corriente común.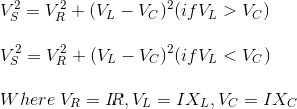
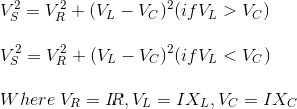

La impedancia para un circuito RLC en serie
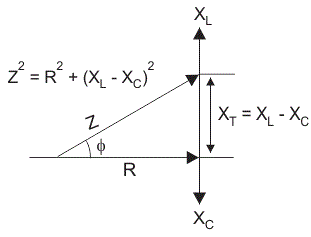

La impedancia Z de un circuito RLC en serie se define como la oposición al flujo de corriente del circuito debido resistencia R, reactancia inductiva, XL y la reactancia capacitiva, XC. Si la reactancia inductiva es mayor que la capacitiva, es decir, XL > XCentonces el circuito RLC tiene un ángulo de fase retardado y si la reactancia capacitiva es mayor que la inductiva, es decir, XC > XL entonces, el circuito RLC tiene un ángulo de fase principal y si tanto el inductivo como el capacitivo son iguales, es decir, XL = XC entonces el circuito se comportará como un circuito puramente resistivo.
Sabemos que
Dónde,
La sustitución de los valores 

Circuito RLC paralelo
En circuito RLC paralelo la resistencia, el inductor y el condensador están conectados en paralelo a través de un suministro de voltaje. El circuito RLC en paralelo es exactamente opuesto al circuito RLC en serie. El voltaje aplicado permanece igual en todos los componentes y la corriente de suministro se divide. La corriente total extraída del suministro no es igual a la suma matemática de la corriente que fluye en el componente individual, pero es igual a su suma vectorial de todas las corrientes, ya que la corriente que fluye en la resistencia, el inductor y el condensador no están en la misma fase entre sí, por lo que no pueden sumarse aritméticamente.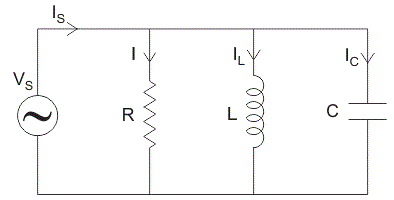

Diagrama de fases del circuito RLC paralelo, IR es la corriente que fluye en la resistencia, R en amperios.
IC es la corriente que fluye en el condensador, C en amperios.
IL es la corriente que fluye en el inductor, L en amperios.
Is es la corriente de suministro en amperios.
En el circuito RLC paralelo, todos los componentes están conectados en paralelo; así que el voltaje de cada elemento es el mismo. Por lo tanto, para dibujar el diagrama de fases, tomemos el voltaje como vector de referencia y todas las demás corrientes, es decir, IR, IC, IL se dibujan en relación a este vector de voltaje. La corriente que pasa por cada elemento se puede encontrar usando Ley actual de Kirchhoffsque establece que la suma de las corrientes que entran en una unión o nodo es igual a la suma de las corrientes que salen de ese nodo.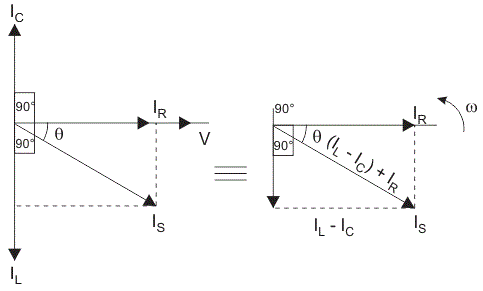

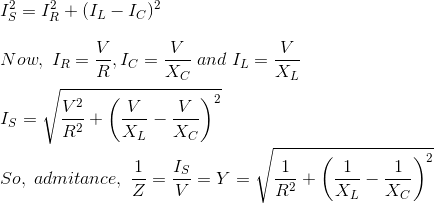
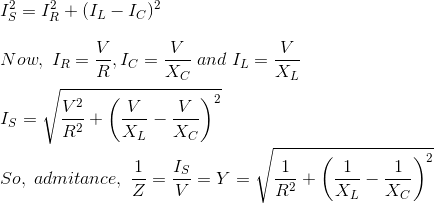
Como se muestra arriba en la ecuación de la impedancia, Z de un circuito RLC paralelo; cada elemento tiene recíproco de impedancia (1 / Z) es decir admisiónY. Así que en el circuito RLC paralelo, es conveniente usar la admitancia en lugar de la impedancia.
Resonancia en el circuito RLC
En un circuito que contiene un inductor y un condensador, la energía se almacena de dos maneras diferentes.
- Cuando una corriente fluye en un inductor, la energía se almacena en campo magnético.
- Cuando un condensador se carga, la energía se almacena en un campo eléctrico estático.
El campo magnético en el inductor está construido por la corriente, que es proporcionada por el condensador de descarga. De manera similar, el condensador se carga por la corriente producida por el colapso del campo magnético del inductor y este proceso continúa una y otra vez, haciendo que la energía eléctrica oscile entre el campo magnético y el campo eléctrico. En algunos casos, a cierta frecuencia llamada frecuencia resonante, la reactancia inductiva del circuito se iguala a la reactancia capacitiva, lo que hace que la energía eléctrica oscile entre el campo eléctrico del condensador y el campo magnético del inductor. Esto forma un oscilador armónico para la corriente. En Circuito RLCla presencia de la resistencia hace que estas oscilaciones desaparezcan con el tiempo y se denomina efecto de amortiguación de la resistencia.
Fórmula para la frecuencia de resonancia
Durante la resonancia, a cierta frecuencia llamada frecuencia resonante, fr.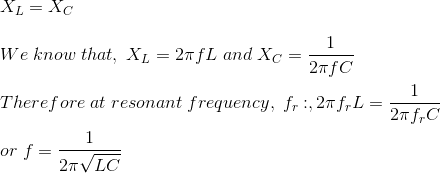
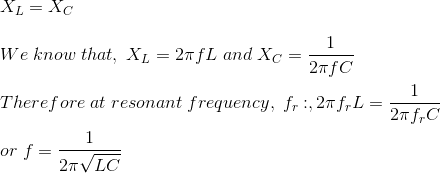
Cuando se produce la resonancia, la reactancia inductiva del circuito se convierte en igual a la reactancia capacitiva, lo que hace que la impedancia del circuito sea mínima en el caso de un circuito RLC en serie; pero cuando la resistencia, el inductor y el condensador están conectados en paralelo, la impedancia del circuito se convierte en máxima, por lo que el circuito RLC en paralelo se denomina a veces anti resonador.
Diferencia entre el circuito RLC en serie y el circuito RLC en paralelo
| S.NO | CIRCUITO DE LA SERIE RLC | CIRCUITO PARALELO RLC |
| 1 | La resistencia, el inductor y el condensador están conectados en serie | La resistencia, el inductor y el condensador están conectados en paralelo |
| 2 | La corriente es la misma en cada elemento | La corriente es diferente en todos los elementos y la corriente total es igual a la suma de los vectores de cada rama de la corriente, es decir, Is2 = IR2 + (IC IL)2 |
| 3 | El voltaje a través de todos los elementos es diferente y el voltaje total es igual a la suma vectorial de los voltajes a través de cada componente, es decir, Vs2 = VR2 + (VL VC)2 | El voltaje de cada elemento sigue siendo el mismo |
| 4 | Para dibujar el diagrama de fases, se toma la corriente como vector de referencia | Para dibujar el diagrama de fases, se toma el voltaje como vector de referencia |
| 5 | El voltaje a través de cada elemento está dado por..: VR= IR, VL = I XL, VC = I XC | La corriente en cada elemento viene dada por: IR = V / R , IC = V / XC , IL = V / XL |
| 6 | Es más conveniente utilizar la impedancia para los cálculos | Es más conveniente usar la admisión para los cálculos |
| 7 | En la resonancia, cuando XL = XCel circuito tiene una impedancia mínima | En la resonancia, cuando XL = XCel circuito tiene una impedancia máxima |
Ecuación del circuito RLC
Considere un Circuito RLC que tienen la resistencia R, el inductor L, y el condensador C conectados en serie y son impulsados por un fuente de tensión V. Deje que Q sea la carga del condensador y la corriente que fluye en el circuito sea I. Aplique La ley de voltaje de Kirchhoffs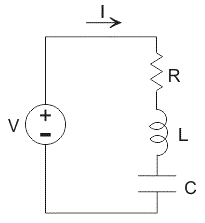

![]()
![]()
En esta ecuación, la resistencia, inductancia, capacitancia y el voltaje son cantidades conocidas pero la corriente y la carga son cantidades desconocidas. Sabemos que una corriente es una tasa de carga eléctrica que fluye, por lo que está dada por![]()
![]()
Diferenciando de nuevo I'(t) = Q (t)![]()
![]()
Diferenciando la ecuación anterior con respecto a t que obtenemos,![]()
![]()
Ahora en el tiempo t = 0, V(0) = 0 y en el tiempo t = t, V(t) = Eosint
Diferenciando con respecto a t obtenemos V'(t) = Eocosto
Sustituir el valor de V'(t) en la ecuación anterior![]()
![]()
Digamos que la solución de esta ecuación es yoP(t) = Asin(t ) y si yoP(t) es una solución de la ecuación anterior, entonces debe satisfacer esta ecuación,![]()
![]()
Ahora sustituye el valor de IP(t) y lo diferenciamos que obtenemos,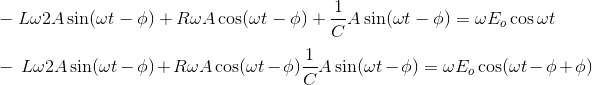
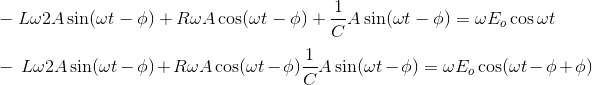
Aplicar la fórmula de cos (A + B) y combinar los términos similares que obtenemos,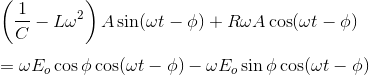
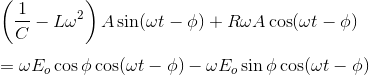
Coincide con el coeficiente de sin(t ) y cos(t ) en ambos lados que obtenemos,![]()
![]()
Ahora tenemos dos ecuaciones y dos incógnitas, es decir, A, y dividiendo las dos ecuaciones anteriores obtenemos,![]()
![]()
Cuadrando y sumando la ecuación anterior, obtenemos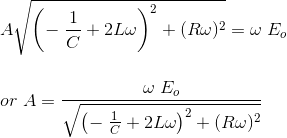
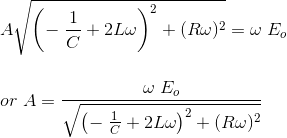
Análisis del circuito RLC usando la transformación de Laplace
Paso 1 : Dibuja un diagrama de fases para un circuito determinado.
Paso 2 : Usar la ley de voltaje de Kirchhoffs en el circuito de serie RLC y la ley de corriente en el circuito paralelo RLC para formar ecuaciones diferenciales en el dominio del tiempo.
Paso 3 : Utilice La transformación de Laplace para convertir estas ecuaciones diferenciales del dominio del tiempo en el dominio s.
Paso 4 : Para encontrar variables desconocidas, resuelve estas ecuaciones.
Paso 5 : Aplicar la transformación inversa de Laplace para convertir las ecuaciones posteriores del dominio s en el dominio del tiempo.
Aplicaciones del circuito RLC
Se utiliza como filtro de paso bajo, filtro de paso alto…filtro pasabanda, filtro pasabanda.., multiplicador de voltaje y oscilador circuito. Se usa para sintonizar la radio o el receptor de audio.


