Más de uno resistencia eléctrica pueden conectarse en serie o en paralelo, además de eso, también pueden conectarse más de dos resistencias en combinación de serie y paralelo ambas. Aquí discutiremos principalmente sobre la combinación en serie y en paralelo.
Resistencias en serie
Supongamos que tienes tres diferentes tipos de resistencias R1, R2 y R3 y los conectas de extremo a extremo como se muestra en la figura de abajo, entonces se referiría como resistencias en serie. En caso de conexión en serie, la resistencia equivalente de la combinación, es la suma de estas tres resistencias eléctricas.
Esto significa que la resistencia entre el punto A y D de la figura de abajo, es igual a la suma de tres resistencias individuales. El actual entra en el punto A de la combinación, también saldrá del punto D ya que no hay otro camino paralelo previsto en el circuito.
Ahora digamos que esta corriente es I. Así que esta corriente pasaré a través de la resistencia R1, R2 y R3. Aplicando La ley de Ohmsse puede encontrar que caídas de tensión a través de las resistencias será V1 = IR1, V2 = IR2 y V3 = IR3. Ahora, si el total voltaje aplicado a través de la combinación de resistencias en seriees V.
Entonces, obviamente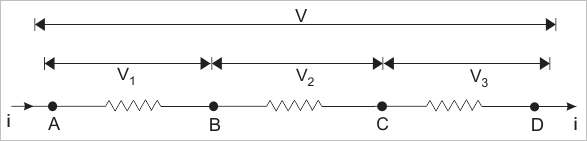

Ya que, la suma de las caídas de voltaje a través de la resistencia individual no es nada más que el igual al voltaje aplicado a través de la combinación.
Ahora bien, si consideramos la combinación total de resistencias como una sola resistencia del valor de resistencia eléctrica R, entonces según la ley de Ohms,
V = IR .(2)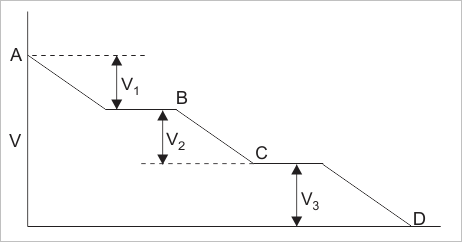

Ahora, comparando la ecuación (1) y (2), obtenemos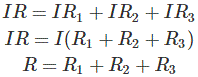
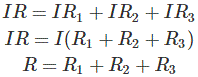
Así, la prueba anterior muestra que la resistencia equivalente de una combinación de resistencias en serie es igual a la suma de la resistencia individual. Si hubiera n número de resistencias en lugar de tres resistencias, la resistencia equivalente sería
Resistencias en paralelo
Digamos que tenemos tres resistencias de valor de resistencia R1, R2 y R3. Estas resistencias están conectadas de tal manera que los terminales derecho e izquierdo de cada resistencia están conectados entre sí, como se muestra en la siguiente figura.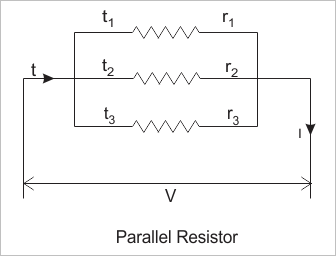

Esta combinación se llama resistencias en paralelo. Si diferencia de potencial eléctrico se aplica a través de esta combinación, entonces dibujará una corriente I (digamos).
Como esta corriente tendrá tres caminos paralelos a través de estos tres resistencias eléctricasla corriente se dividirá en tres partes. Diga corrientes I1, I1 y yo1 pasar a través de la resistencia R1, R2 y R3 respectivamente.
Donde el total de la corriente de la fuente
Ahora, a partir de la figura está claro que, cada uno de los resistencias en paraleloestá conectado a través de la misma fuente de tensiónel caídas de tensión a través de cada resistencia es la misma, y es igual al voltaje de suministro V (digamos).
Por lo tanto, según La ley de Ohms,![]()
![]()
Ahora, si consideramos que la resistencia equivalente de la combinación es R.
Entonces..,
Ahora poniendo los valores de I, I1, I2 y yo3 en la ecuación (1) que obtenemos,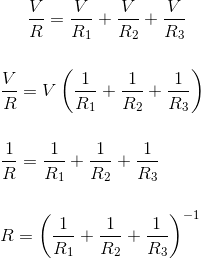
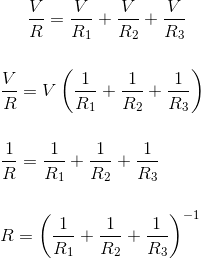
La expresión anterior representa la resistencia equivalente de la resistencia en paralelo. Si hubiera n número de resistencias conectadas en paralelo, en lugar de tres resistencias, la expresión de resistencia equivalente sería![]()
![]()




