Los circuitos de CA suelen ser trifásicos para distribución eléctrica y transmisión eléctrica …propósitos. Los circuitos monofásicos se usan comúnmente en nuestro sistema de suministro doméstico.
El total la potencia de un trifásico El circuito de CA es igual a tres veces la potencia monofásica.
Así que si la potencia en una fase simple de un sistema trifásico es P, entonces la potencia total del sistema trifásico sería de 3P (siempre que el sistema trifásico esté perfectamente equilibrado).
Pero si el sistema trifásico no está exactamente equilibrado, entonces la potencia total del sistema sería la suma de la potencia de las fases individuales.
Supongamos que, en un sistema trifásico, la potencia en la fase R es PR en la fase Y es PY y en la fase B es PBentonces la potencia total del sistema sería
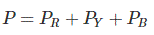
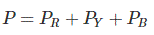
Esta es una simple suma escalar, ya que el poder es una cantidad escalar. Esta es la estación, si consideramos sólo una fase durante el cálculo y análisis de energía trifásica…es suficiente.
Consideremos que la red A está conectada eléctricamente con la red B, como se muestra en la siguiente figura:
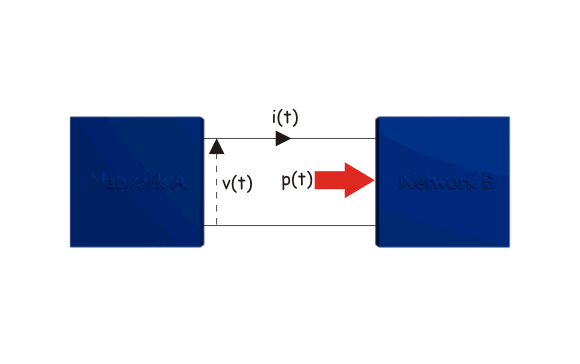

Consideremos la expresión de la forma de onda de voltaje de un sistema monofásico es:


Donde V es la amplitud de la forma de onda, es la velocidad angular de propagación de la onda.
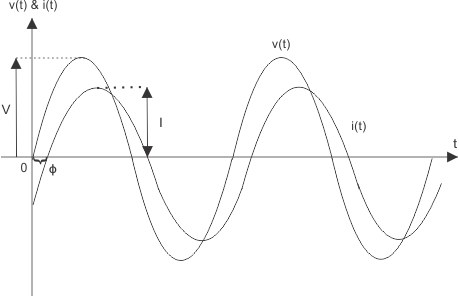
Ahora, considera el actual del sistema es i(t) y esta corriente tiene una diferencia de fase con la voltaje por un ángulo . Eso significa que la onda de corriente se propaga con un retraso radiante con respecto al voltaje. La forma de onda del voltaje y de la corriente puede representarse gráficamente como se muestra a continuación:
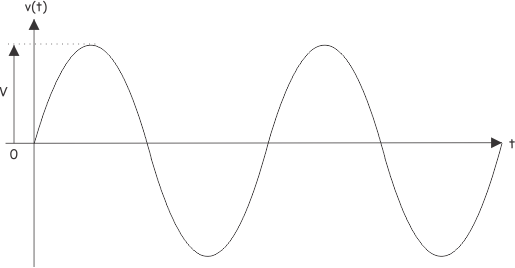

La forma de onda de la corriente en este caso puede representarse como:

Ahora, la expresión del poder instantáneo,
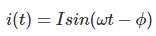
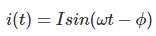
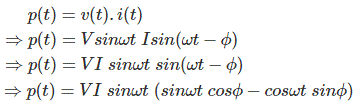
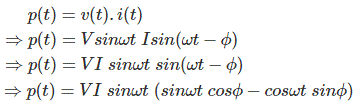
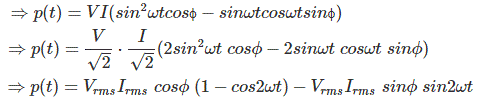
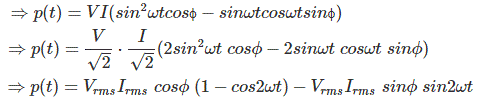
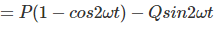
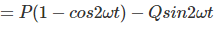
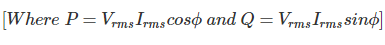
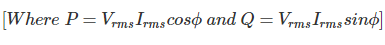
[donde Vrms y yorms es el valor cuadrático medio del voltaje y la forma de onda de la corriente]
Ahora, trazaremos el término P contra el tiempo,
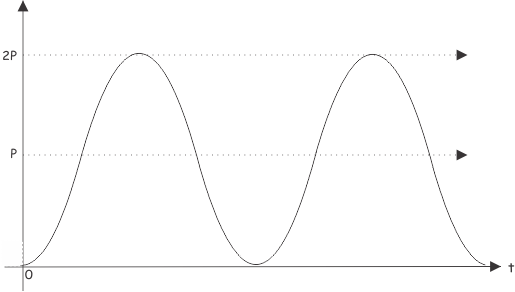

Se ve en el gráfico que, el término P no tiene ningún valor negativo. Por lo tanto, tendrá un valor promedio distinto de cero. Es sinusoidal con una frecuencia dos veces superior a la del sistema. Ahora vamos a graficar segundo término de la ecuación de poder, es decir, Q.
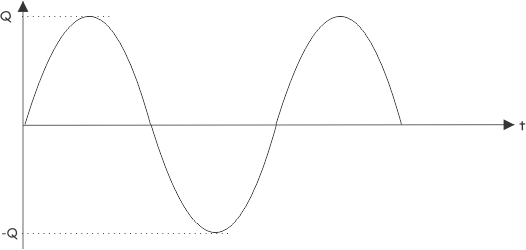

Esto es puramente sinusoidal y tiene un valor promedio de cero. Así que de estos dos gráficos, está claro que P es el componente de la energía en un circuito de CA, que en realidad se transporta de la red A a la red B. Esta energía se consume en la red B como energía eléctrica.
Q por otro lado no fluye realmente de la red A a la red B. Más bien oscilar entre la red A y B. Este también es un componente de la energía, que fluye en realidad dentro y fuera del inductor, condensador como elementos de almacenamiento de energía de la red.
Aquí, P se conoce como la parte real o activa de la potencia y Q se conoce como la parte imaginaria o reactiva de la potencia.
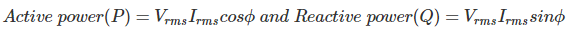
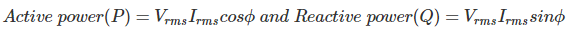
Por lo tanto, P se llama poder real o poder activo, y Q se llama poder imaginario o poder activo. La unidad de potencia activa es el vatio, mientras que la unidad de potencia reactiva es el voltaje amperio reactivo o VAR.
Ya lo hemos considerado,
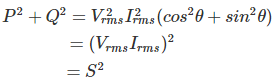
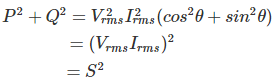
donde, S es el producto del valor medio de la raíz del voltaje y actual es decir.
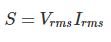
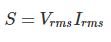
Este producto del valor RMS de voltaje y corriente de un sistema es referido ya que la potencia aparente es el voltaje en amperios o en VA. Así que..,
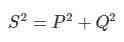
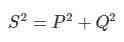
Esto puede representarse en forma compleja como
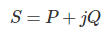
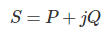
Una vez más, la expresión del poder real es
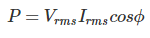
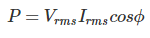
donde está el ángulo entre voltaje y el fásor actual. Así que..,
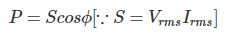
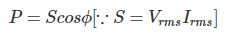
Así que, aquí en la expresión P, cos es el factor que determina el componente de potencia real de una potencia aparente S.
Por eso el término «cos» en la expresión del poder real se llama factor de potencia. Tanto para el valor positivo como para el negativo de , cos es siempre positivo.
Esto implica que, independientemente del signo de (que depende de si la corriente se retrasa o conduce el voltaje) la potencia real es siempre positiva.
Esto significa que fluye desde el extremo emisor (Red A) hasta el extremo receptor (Red B). También hemos mostrado lo mismo anteriormente al observar la forma de onda para la potencia real.
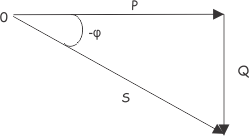
Ahora bien, si la corriente conduce el voltaje, entonces el ángulo entre el voltaje y el fásor de la corriente es negativo, tomando el fásor del voltaje como referencia:
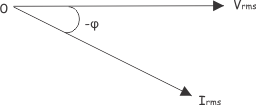

En ese caso el componente reactivo de la energía es negativo,
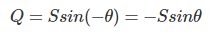
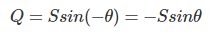
Triángulo de Poder
La relación entre la potencia aparente y la potencia activa y la potencia reactiva puede representarse en forma trigonométrica como se muestra a continuación.

Ahora, si actual está retrasando el voltaje el ángulo entre el voltaje y el fásor de la corriente es positivo, tomando el fásor del voltaje como referencia.
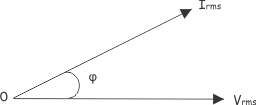

En este caso, el componente reactivo de la energía es positivo. Ya que,
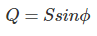
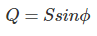
El triángulo de poder se representa como se muestra a continuación.
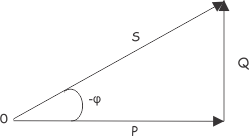

Si la impedancia de la red es capacitiva, la corriente conduce la voltaje y en caso de inductivo …la red de la corriente se queda sin voltaje. Así que podemos concluir que la potencia reactiva es negativa en el caso de la reactancia capacitiva y es positiva y en el caso de la reactancia inductiva.
Si la red es puramente resistiva, no habría ninguna diferencia angular entre la corriente y el voltaje. Por lo tanto,
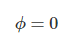
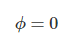
Así que la potencia reactiva en este caso sería,
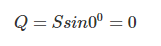
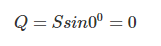
Por lo tanto, no hay energía reactiva generada o consumida en la red.