¿Qué es la trama de Nyquist
A La trama de Nyquist (o Diagrama de Nyquist) es un gráfico de respuesta en frecuencia utilizado en ingeniería de control y el procesamiento de la señal. Las gráficas de níquel se utilizan comúnmente para evaluar la estabilidad de un sistema con retroalimentación. En las coordenadas cartesianas, la parte real de la función de transferencia se traza en el eje X, y la parte imaginaria se traza en el eje Y. La frecuencia se barre como un parámetro, resultando en un gráfico basado en la frecuencia. El mismo gráfico de Nyquist puede describirse utilizando coordenadas polares, donde la ganancia de la función de transferencia es la coordenada radial, y la fase de la función de transferencia es la coordenada angular correspondiente.
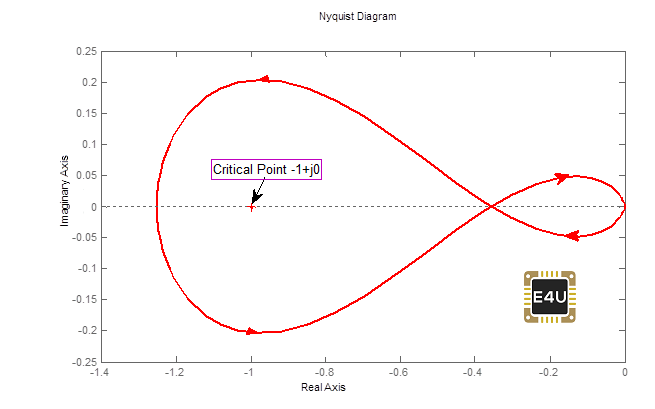

El análisis de estabilidad de una retroalimentación sistema de control se basa en la identificación de la ubicación de las raíces de la ecuación característica en el plano s. El sistema es estable si las raíces se encuentran en el lado izquierdo del plano s. La estabilidad relativa de un sistema puede determinarse utilizando métodos de respuesta en frecuencia como el La trama de Nyquist y La trama de Bode.
El Criterio de estabilidad del níquel se utiliza para identificar la presencia de raíces de una ecuación característica en una región específica del plano s. Para comprender una La trama de Nyquist primero tenemos que aprender sobre algunas de las terminologías. Obsérvese que un camino cerrado en un plano complejo se llama contorno.
Camino de Nyquist o Contorno de Nyquist
El Contorno de Nyquist es un contorno cerrado en el plano S que encierra completamente la mitad derecha del plano S. Para encerrar la RHS completa del plano s, se dibuja un gran semicírculo con diámetro a lo largo del eje j y centro en el origen. El radio del semicírculo se trata como un círculo de Nyquist.
Cercado de Nyquist
Se dice que un punto está rodeado por un contorno si se encuentra dentro del contorno.
Cartografía de Nyquist
El proceso por el cual un punto en el plano s se transforma en un punto en el plano F(s) se llama mapeo y F(s) se llama función de mapeo.
Cómo dibujar la trama de Nyquist
Una trama de Nyquist puede ser dibujada usando los siguientes pasos:
- Paso 1 Busca los polos de G(s) H(s) del eje j incluyendo el de origen.
- Paso 2 Seleccione el contorno de Nyquist apropiado a) Incluya toda la mitad derecha del plano s dibujando un semicírculo de radio R con R tiende al infinito.
- Paso 3 Identificar los diversos segmentos del contorno con referencia a El camino de Nyquist
- Paso 4 Realice el mapeo segmento por segmento sustituyendo la ecuación por el segmento respectivo en la función de mapeo. Básicamente, tenemos que esbozar los diagramas polares del segmento respectivo.
- Paso 5 La cartografía de los segmentos son generalmente imágenes espejo de la cartografía de la trayectoria respectiva del eje imaginario +ve.
- Paso 6 El camino semicircular que cubre la mitad derecha del plano s, generalmente se mapea en un punto del plano G(s) H(s).
- Paso 7… Interconecte todos los mapas de los diferentes segmentos para obtener el requerido Diagrama de Nyquist.
- Paso 8 Anote el número de vueltas en el sentido de las agujas del reloj alrededor de (-1, 0) y decida la estabilidad por N = Z P
![]()
![]()
es la función de transferencia de bucle abierto (O.L.T.F)
![]()
![]()
es la función de transferencia en bucle cerrado (C.L.T.F)
N(s) = 0 es el cero de bucle abierto y D(s) es el polo de bucle abierto
Desde el punto de vista de la estabilidad, ningún polo de bucle cerrado debería estar en el lado derecho del plano S. La ecuación de características 1 + G(s) H(s) = 0 denota los polos de bucle cerrado .![]()
![]()
Ahora como 1 + G(s) H(s) = 0 por lo que q(s) también debería ser cero.![]()
![]()
Por lo tanto, desde el punto de vista de la estabilidad, los ceros de q(s) no deben estar en el RHP del plano s.
Para definir la estabilidad se considera todo el RHP (Right-Hand Plane). Asumimos un semicírculo que encierra todos los puntos del RHP considerando el radio del semicírculo R tiende al infinito. [R ].
El primer paso para comprender la aplicación de El criterio de Nyquist en relación con la determinación de la estabilidad de los sistemas de control es la cartografía del plano s al plano G(s) H(s). s se considera una variable compleja independiente y el valor correspondiente de G(s) H(s) es la variable dependiente trazada en otro plano complejo llamado plano G(s) H(s).
Así, para cada punto del plano s, existe un punto correspondiente en el plano G(s) H(s). Durante el proceso de mapeo, la variable independiente s se varía a lo largo de una trayectoria especificada en el plano s y se unen los puntos correspondientes en el plano G(s)H(s). Esto completa el proceso de mapeo desde el plano s al plano G(s)H(s).
Criterio de estabilidad del níquel dice que N = Z P. Donde N es el número total de cercos sobre el origen, P es el número total de polos y Z es el número total de ceros.
Caso 1: N = 0 (sin encierro), así que Z = P = 0 y Z = P
Si N = 0, P debe ser cero, por lo tanto el sistema es estable.
Caso 2: N > 0 (encierro en el sentido de las agujas del reloj), por lo que P = 0, Z 0 y Z > P
En ambos casos el sistema es inestable.
Caso 3: N < 0 (encierro en el sentido contrario a las agujas del reloj), así que Z = 0, P 0 y P > Z
El sistema es estable.