Las series de Fourier de un vistazo
Se dice que una señal temporal continua x(t) es periódica si hay un valor positivo no nulo de T para el cual

Como sabemos, cualquier señal periódica puede clasificarse en sinusoides armónicamente relacionadas o en exponenciales complejas, siempre que satisfaga la Condiciones de los Dirichlets. Esta representación descompuesta se llama SERIE CUATRO.
Dos tipos de Series de Fourier representación están ahí. Ambos son equivalentes entre sí.
- Serie de Fourier exponencial
- Serie de Fourier trigonométrica
Ambas representaciones dan el mismo resultado. Dependiendo del tipo de señal, elegimos cualquiera de las representaciones según nuestra conveniencia.
Serie de Fourier exponencial
Una señal periódica se analiza en términos de Serie de Fourier exponencial en las siguientes tres etapas:
- Representación de la señal periódica.
- Espectros de amplitud y fase de una señal periódica.
- Contenido de energía de una señal periódica.
Representación de la señal periódica
Una señal periódica en las Series de Fourier puede ser representada en dos dominios temporales diferentes:
- Dominio de tiempo continuo.
- Dominio de tiempo discreto.
Dominio de tiempo continuo
El complejo Serie de Fourier exponencial representación de una señal periódica x(t) con el período fundamental To está dada por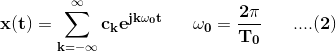
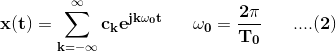
Donde, C es conocido como el Complejo del Coeficiente de Fourier y se da por,![]()
![]()
Donde0T0denota la integral en cualquier período y, 0 a T0 o T0/2 a T0/2 son los límites comúnmente utilizados para la integración.
La ecuación (3) se puede deducir multiplicando ambos lados de la ecuación (2) por e(-jl0t) e integrar durante un período de tiempo ambos lados.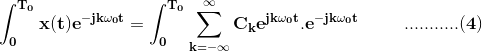
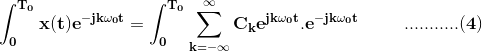
Al intercambiar el orden de suma e integración en R.H.S., obtenemos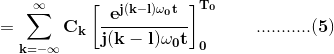
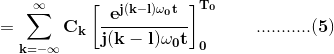
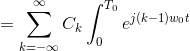
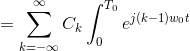
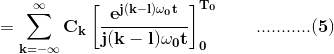
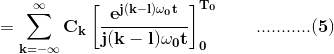
Cuando, kl, el lado derecho de (5) evaluado en el límite inferior y superior da cero. Por otro lado, si k=l, tenemos![]()
![]()
Por consiguiente, la ecuación (4) se reduce a![]()
![]()
![]()
![]()
![]()
![]()
que indica el valor medio de x(t) a lo largo de un período.
Cuando x (t) es real,
Donde, * indica conjugar
Dominio de tiempo discreto
La representación de Fourier en discreto es muy similar a la representación de Fourier de la señal periódica del dominio del tiempo continuo.
La representación de la serie discreta de Fourier de una secuencia periódica x[n] con el período fundamental No está dada por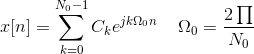
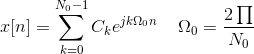 ¿Dónde, Ckson los coeficientes de Fourier y están dados por
¿Dónde, Ckson los coeficientes de Fourier y están dados por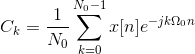
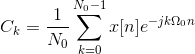
Esto puede ser derivado de la misma manera que lo derivamos en el dominio del tiempo continuo.
Espectros de amplitud y fase de una señal periódica
Podemos expresar el Complejo de Coeficiente de Fourier, Ck como

Una trama de |Ck| contra la frecuencia angular w se llama el espectro de amplitud de la señal periódica x(t), y una gráfica dekversus w se llama el espectro de fase de x(t). Dado que el índice k asume sólo números enteros, los espectros de amplitud y de fase no son curvas continuas sino que aparecen sólo en las frecuencias discretas k0Por lo tanto, se denominan espectros de frecuencia discretos o espectros de línea.
Para una señal periódica real x (t) tenemos C-k = Ck*. Así,

Por lo tanto, el espectro de amplitud es una función par de , y el espectro de fase es una función impar de 0 para una señal periódica real.
Contenido de energía de una señal periódica
Promedio Contenido de energía de una señal periódica está dada por![]()
![]()
Si x (t) está representada por la compleja Serie de Fourier exponencial, entonces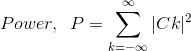
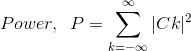
Esta ecuación se conoce como identidad de Parsevals o Teorema de Parsevals.
