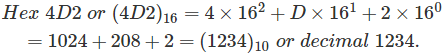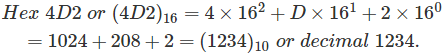El sistema hexadecimal es un sistema numérico con base 16. Este sistema numérico es muy utilizado por los sistemas informáticos modernos.
Ya sabemos sobre el sistema de números decimales, sistema numérico binario y sistema de número octal. Como esos hay otro sistema de números llamado sistema de números hexadecimales. Como su nombre indica, hay 16 símbolos en este sistema numérico empezando por el 0. Antes de explicar el sistema numérico debemos saber por qué este sistema numérico llegó a existir. La tendencia natural de los humanos es utilizar el sistema numérico decimal porque están familiarizados con él, ya que el uso del 0 es muy fácil y las operaciones son fáciles de usar. Y los sistemas informáticos utilizaron antes sistemas binarios porque sólo hay dos estados de encendido y apagado.
Pero a medida que la dependencia de la computadora crecía y se necesitaban desarrollar diferentes programas matemáticos y diferentes softwares, surgió la necesidad de desarrollar un sistema numérico con una base mayor que el decimal y se eligió el 16 porque los bits, bytes son múltiplos de él. Hoy en día este sistema numérico se utiliza en HTML y CSS, en ellos se utilizan notaciones hexadecimales. Este sistema numérico fue utilizado por primera vez alrededor de 1956 en el ordenador Bendix G-15.
Ahora vamos a la representación de sistema de números hexadecimalesEn este sistema numérico hay 16 dígitos básicos con los que se pueden representar todos los números, estos son 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F los primeros 10 dígitos son similares al sistema numérico decimal pero los últimos 6 dígitos representan 10, 11, 12, 13, 14 y 15 respectivamente. Cualquier número en el sistema numérico hexadecimal puede ser convertido en números de otro sistema numérico muy fácilmente, los procedimientos se dan en el siguiente artículo.

Aquí en el sistema decimal, usamos el símbolo 1 y 0 lado a lado que es 10 para representar +
Eso es nueve más uno. Después de eso tendremos 11, luego 12 y así sucesivamente. Esto significa que después del nueve o el 9 traemos el primer dígito no cero del símbolo que es 1 en el lado izquierdo y repetimos todos los símbolos del 0 al 9 en su lado derecho para representar los siguientes diez números más altos del diez al diecinueve (10 19). Después del 19 ponemos el 2 a la izquierda y repetimos de nuevo el 0 al 9 para representar los siguientes diez números más altos del veinte al veintinueve (20 29). Sistema de números decimales es un sistema numérico muy básico ya que se utilizan diez símbolos o dígitos en diferentes combinaciones para representar todos los números, se dice que este sistema es de base diez (10). Ahora piensa en un sistema numérico en el que se te dice que uses dieciséis símbolos en lugar de diez. Entonces, ¿cuál será su construcción básica del nuevo sistema numérico? Para eso primero tenemos que encontrar 16 símbolos para representar los dígitos básicos de ese nuevo sistema numérico.
Podemos crear nuevas series de símbolos para eso, pero si lo hacemos será muy difícil de recordar. Esa dificultad puede ser resuelta si usamos símbolos comúnmente usados para ese propósito. Así que podemos usar simplemente del 0 al 9 del sistema decimal para representar los primeros diez dígitos del 0 al 9 de este nuevo sistema numérico. Pero para los otros 6 dígitos más altos no hay símbolos disponibles en el sistema decimal, así que tenemos que buscarlos en algún sistema de uso común. Podemos obtenerlos fácilmente de nuestro sistema alfabético, lo que significa que podemos usar A, B, C, D, E y F como los siguientes 6 dígitos superiores (del 10 al 15) en este nuevo sistema numérico. El sistema en el que se utilizan un total de 16 dígitos básicos se conoce como sistema numérico hexadecimal.
| A | • | • | • | • | • | • | • | • | • | • | |||||
| B | • | • | • | • | • | • | • | • | • | • | • | ||||
| C | • | • | • | • | • | • | • | • | • | • | • | • | |||
| D | • | • | • | • | • | • | • | • | • | • | • | • | • | ||
| E | • | • | • | • | • | • | • | • | • | • | • | • | • | • | |
| F | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • |
En el sistema hexadecimal usamos 16 símbolos para representar todos los números. Estos símbolos son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Después de F usamos 10 para el siguiente número 16. Luego el siguiente incremento es el 11 que se utiliza para representar el siguiente número natural 17 y así sucesivamente.
Por lo tanto, en el sistema hexadecimal justo después de F, el primer dígito se convierte en 1 y el segundo dígito se repetirá de 0 a F uno por uno para representar los números naturales 16 a 31.
Eso significa, 10 16, 11 17, 12 18, 13 19, 14 20, 15 21, 16 22, 17 23, 18 24, 19 25, 1A 26, 1B 27, 1C 28, 1D 29, 1E 30, 1F 31. Después de esto el primer dígito aumentará a 2 y de nuevo el segundo dígito se repetirá de 0 a F uno por uno para representar los números naturales 32 a 47 y así sucesivamente.
Conversión de decimal a hexadecimal
Como ya hemos dicho en los artículos anteriores sobre los sistemas de números, todos los sistemas de números están interrelacionados, como los números decimales y hexadecimales. Cualquier número en el sistema numérico decimal puede convertirse en el sistema numérico hexadecimal. A continuación se expone el procedimiento.
Si intentamos entender el procedimiento con un ejemplo y paso a paso, será más fácil y mejor para nosotros.
Tomemos primero cualquier número decimal, supongamos que hemos tomado 7510 y ahora queremos convertirlo en un número hexadecimal, primero tenemos que dividirlo por 16.
75/16 = cociente 4, resto 11
Como el cociente es menor de 16, tenemos que parar aquí y el número hexadecimal equivalente será
4B8 = 7510
Ahora discutiremos el método para un número ligeramente mayor,
Supongamos que el número es 169310
Ahora lo dividimos por 16
1693/16 = cociente = 105, resto = 13(D)
Ahora tenemos que dividir el cociente de nuevo por 16 y ver el resultado
105/16 = cociente = 6 resto = 9
Como el cociente es menor de 16, la parte del cálculo se ha completado y ahora podemos escribir directamente el resultado
169310 = 69D16
Así que el número decimal se ha convertido en un número hexadecimal.
De la explicación anterior se puede entender que, el número hexadecimal es la suma de productos de diferentes dígitos con sus respectivos multiplicadores. Los multiplicadores son 160, 161, 162…de la mano derecha o de la lista de bits significativos (LSB). Tengamos un ejemplo 4D2 y esto se expresaría como![]()
![]()
Si dividimos el decimal 1234 por 16, obtendremos 77 como cociente y 2 como resto. Entonces, si dividimos el decimal 77 por 16, obtendremos 4 como cociente y 13 o D como resto. Ahora si escribimos lado a lado desde el último cociente hasta el primer recordatorio, obtendremos 4D2 que es hexadecimal o equivalente hexagonal del número 1234.
| Para ello dividimos 1234 por la base 16 y obtenemos 77 como el cociente y 2 como el resto. | 16 | 1234 | →2 |
| Dividir de nuevo 77 por 16 y obtenemos 4 como el cociente y 13 o D como el resto. | 16 | 77 | D |
| 4 |
Presentación en vídeo de la conversión de decimal a hexadecimal
Conversión hexadecimal a decimal
De manera similar, cualquier número hexadecimal puede ser convertido en un número decimal. Veremos el proceso con un ejemplo.
Pero antes de comenzar debe aclararse que antes de la conversión de un número hexadecimal todas las letras del número deben tomarse como sus valores numéricos en el sistema numérico decimal, es decir, si un dígito en un número hexadecimal es A, entonces debemos tomarlo como 10, ahora un ejemplo aclarará todo el procedimiento.
Tomemos cualquier número hexadecimal 45B116tenemos que convertirlo en número decimal, así que empezando por el dígito más a la derecha tenemos que empezar a multiplicar los dígitos con una potencia ascendente de 16 empezando por 0.
Así que el número tomado será operado como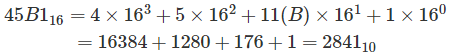
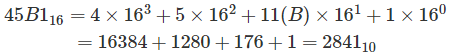
En este procedimiento cualquier número hexadecimal puede convertirse en número decimal.
El valor del número hexadecimal se determina multiplicando cada dígito del número hexadecimal por su respectivo multiplicador. Empezamos desde LSB o la mayoría de los dígitos de la derecha y los multiplicamos por 160…y luego llegar al siguiente dígito a la izquierda de LSB y multiplicarlo por 16…1 y después de eso llegamos al dígito más a la izquierda y multiplicamos 162 con él. Continuamos esto hasta el MSB o la parte izquierda. Añadimos todo este producto y finalmente obtenemos el equivalente decimal del número hexadecimal. Este es uno de los procesos más fáciles de conversión hexadecimal a decimal.
Piensa en el hexágono número 4D2. Aquí la parte menos significativa del número es el 2, así que lo multiplicaremos por 16.0 o 1. Luego ven al siguiente dígito de la izquierda que es D o 13 y lo multiplicaremos por 16.1 o 16. Por último, multiplicaremos el dígito más a la izquierda o MSB, es decir, 4 con 162. Ahora si sumamos estos tres términos, finalmente obtendremos el equivalente dedimal de dicho número hexadecimal. Esto es lo que la conversión hexadecimal a decimal
Por lo tanto,