A veces toda la información en el dominio del tiempo no es suficiente. Esto nos hace pasar al dominio de la frecuencia de la señal para extraer más información sobre la misma. Este movimiento de un dominio a otro dominio se conoce como transformación. Para cambiar el dominio de la señal del tiempo a la frecuencia tenemos muchas herramientas. Series de Fourier y Transformación de Fourier son dos de las herramientas en las que descomponemos la señal en sinusoides armónicamente relacionadas. Con tal descomposición, se dice que una señal se representa en el dominio de la frecuencia.
La mayoría de las señales prácticas pueden descomponerse en sinusoides. Tal descomposición de señales periódicas se llama Series de Fourier.
Análisis de frecuencia
Al igual que una luz blanca puede descomponerse en siete colores, una señal periódica también puede descomponerse en una suma ponderada de frecuencias armónicamente relacionadas. Esta suma ponderada lineal de sinusoides armónicamente relacionados o exponenciales complejos se conoce como Series de Fourier o Transformación. En general, la descomposición de cualquier señal en sus componentes relacionados con la frecuencia se llama análisis de frecuencia. Al igual que el análisis de una luz en colores es en realidad una forma de análisis de frecuencia, por lo tanto las series de Fourier y la transformación de Fourier son también herramientas de análisis de frecuencia.
Esto puede ser más claro a partir de lo siguiente.
Supongamos que si pasamos una luz a través de un prisma, se divide en siete colores VIBGYOR. Cada color tiene una frecuencia particular o un rango de frecuencias. De la misma manera, si pasamos una señal periódica a través de una herramienta de Fourier, que desempeña el papel de prisma, la señal se descompone en una serie de Fourier.

Analogía de Señales y Vectores
Un vector de N dimensiones necesita N dimensiones para su representación. Como una hormiga que se mueve sobre una mesa necesita dos dimensiones para la representación de su posición sobre la mesa, es decir, x e y. También estamos familiarizados con el sistema de coordenadas i, j, k para una representación vectorial en tres dimensiones. Esta unidad vectorial i, j y k son ortogonales entre sí. De la misma manera, si tratamos una señal como un vector multidimensional, necesitamos muchas más dimensiones que son ortogonales entre sí. Fue el genio de J. B. J. Fourier quien inventó las multidimensiones, que son ortogonales entre sí. Son sinusoides con sinusoides armónicamente relacionadas o exponenciales complejas. Considere las dimensiones (también llamadas bases)
sin0t sin20t sin30t sin40t ..sinn0t
cos0t cos20t cos30t cos40t..cosn0t
Por lo tanto, todos los sinn0t son ortogonales con Sinm0t (nm) y, por lo tanto, podemos usar sin0t, sin20t como las dimensiones primarias (también llamadas bases) para expresar una señal periódica. De manera similar, también podemos usar cos0t, cos20t, cos30t como las dimensiones adicionales cuando las dimensiones sin0t no pueden ser utilizadas. Veremos que para las señales pares sólo serán adecuados los términos coseno y para las señales impares sólo serán adecuados los términos seno. Para una señal periódica ni par ni impar, usamos ambos términos, seno y coseno.
NOTA
Sólo las señales periódicas pueden ser representadas como series de Fourier siempre que la señal siga las condiciones de los Dirichlets. Para las señales no periódicas, tenemos la herramienta de transformación de Fourier que transforma la señal del dominio del tiempo al dominio de la frecuencia.
La resolución de la señal en sus frecuencias armónicamente relacionadas se conoce como Análisis de Fourier mientras que la inversa, es decir, la recombinación, se conoce como Sistema de Fourier.
Condiciones de los Dirichlets
x (t) es absolutamente integrable en cualquier período, es decir,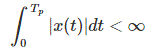
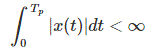
x (t) tiene un número finito de máximos y mínimos dentro de cualquier intervalo finito de t.
x (t) tiene un número finito de discontinuidades dentro de cualquier intervalo finito de t, y cada una de estas discontinuidades es finita.
Tenga en cuenta que las condiciones de los Dirichlets son suficientes pero no necesarias para la representación de las series de Fourier.