Consideremos un solo átomo del número atómico Z. Digamos que +e culombio es la carga de cada protón en el núcleo y -e culombio es la carga de cada electrón que rodea el núcleo. Todos los electrones en órbita del átomo forman una nube esférica de carga negativa que rodea el núcleo de carga positiva. La carga del núcleo es +Ze coulomb y la carga de la nube negativa de electrones es -Ze coulomb. Supongamos también que la carga negativa de la nube de electrones está distribuida homogéneamente en una esfera de radio R. Cuando no hay influencia de ninguna campo eléctricoel centro de esta esfera y el centro del núcleo del átomo coinciden. Ahora, digamos que un campo eléctrico externo de intensidad E voltios por metro se aplica en el átomo. Debido a este campo eléctrico externo, el núcleo del átomo se desplaza hacia la intensidad negativa del campo y la nube de electrones se desplaza hacia la intensidad positiva del campo.
Como debido a la influencia del campo eléctrico externo el centro del núcleo y el centro de la nube de electrones están separados, se desarrollará una fuerza de atracción entre ellos de acuerdo con Ley de Coulombes. Digamos que a la distancia de separación del centro del núcleo y la nube de electrones, x, se establece el equilibrio. Esto significa que a la distancia de separación x, las fuerzas que actúan sobre el núcleo o nube de electrones debido al campo eléctrico externo y debido a la ley de Coulomb se vuelven iguales y opuestas. Es obvio que el radio del núcleo es mucho más que el de la nube de electrones. Así que con respecto a la nube de electrones el núcleo puede considerarse como carga puntual. Por lo tanto, la fuerza electrostática que actúa en el núcleo sería +E.Z.e. Ahora el núcleo se ha desplazado del centro de la nube de electrones por una distancia x.
De acuerdo con Teorema de Gaussla fuerza debida a la nube de electrones negativos que actúa sobre el núcleo positivo sólo sería debida a la porción de la nube encerrada en la esfera de radio x. La porción de la nube fuera de la esfera de radio x no aplica ninguna fuerza sobre el núcleo. Ahora bien, el volumen de la esfera de radio x es (4/3)x3 y el volumen de la esfera de radio R es (4/3)R3.
Ahora la carga negativa total de la nube de electrones es -Ze y ya hemos considerado que está uniformemente distribuida en todo el volumen de la nube.
Por lo tanto, la cantidad de carga negativa encerrada por la esfera de radio x es,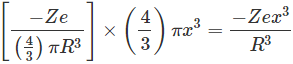
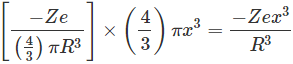
Sólo esta carga aplicará la fuerza coulómbica en el núcleo. Así que, de acuerdo con Ley de Coulombesla fuerza sería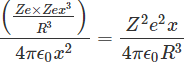
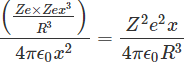
En condición de equilibrio,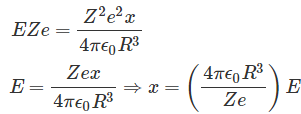
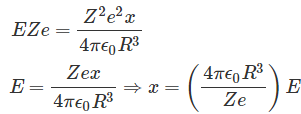
Ahora el momento dipolar del núcleo es Zex como momento dipolar es el producto de la carga del núcleo y la distancia de desplazamiento. Ahora, poniendo la expresión de x en la expresión del momento del dipolo, tenemos,![]()
![]()
La polarización se define como el número de momentos dipolares por unidad de volumen del material. Si N es el número de momentos dipolares por unidad de volumen, la polarización sería,
De la expresión anterior se desprende que el polarización electrónica o la polarización atómica depende del radio (o volumen) de la átomo y el número de átomos presentes en el volumen unitario del material.
