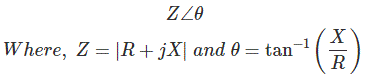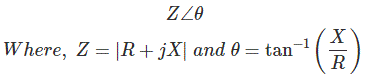El actual lags 90 (eléctrico) con respecto a la aplicación voltaje en un circuito puramente inductivo. El actual cables 90 (eléctricos) con respecto a la aplicación de voltaje en un circuito puramente capacitivo. El actual no se retrasa ni se adelanta con respecto a la aplicación voltaje en un circuito puramente resistivo. En un circuito práctico donde tanto la reactancia inductiva como la capacitiva están presentes junto con resistencia o bien de reactancia capacitiva o inductiva presenta junto con resistenciahabrá un efecto de avance o retroceso en el actual del circuito dependiendo del valor de la reactancia y resistencia del circuito. En el circuito de CA, el efecto acumulativo de la reactancia y resistencia se denomina impedancia. El impedancia normalmente se indica con la letra Z. El valor de impedancia se representa como
![]()
![]()
Donde R es el valor del circuito resistencia y X es el valor de la reactancia del circuito.
El ángulo entre la aplicación voltaje y la corriente es
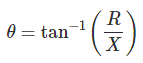
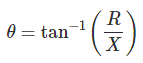
La reactancia inductiva se toma como positiva y la capacitiva como negativa.
La impedancia puede representarse de forma compleja. Esto es
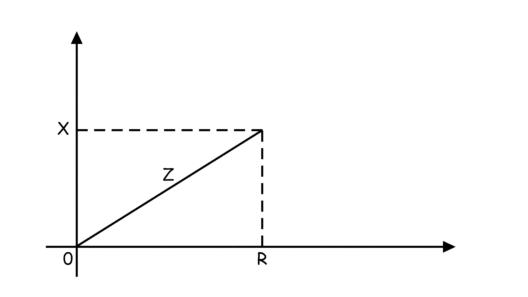

La parte real de una impedancia compleja es la resistencia y la parte imaginaria es la reactancia del circuito.
Apliquemos un voltaje sinusoidal Vsint a través de un puro inductor de inductancia L Henry.
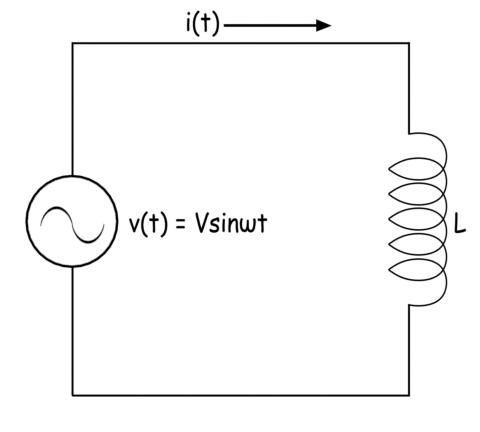

La expresión de la corriente a través de la inductor es
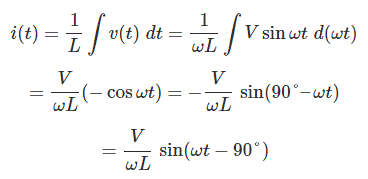
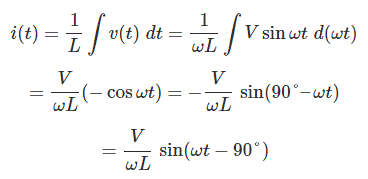
Desde la expresión de la forma de onda de la corriente a través de la inductor está claro que la corriente se retrasa el voltaje aplicado en un 90 (eléctrico).
Ahora apliquemos el mismo voltaje sinusoidal Vsint a través de un puro condensador de capacitancia C farad.
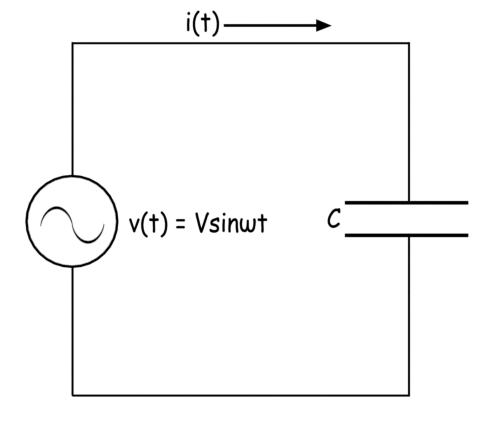

La expresión de la corriente a través de la condensador es
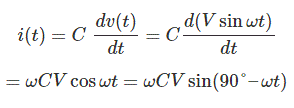
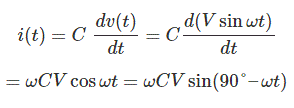
Desde la expresión de la forma de onda de la corriente a través de la condensador está claro que la corriente conduce el voltaje aplicado por 90 (eléctrico).
Ahora conectaremos la misma fuente de voltaje a través de una resistencia pura de valor R ohm.
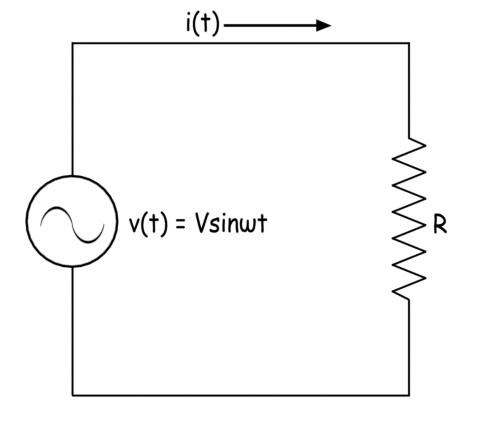

Aquí la expresión de la corriente a través de la resistencia sería
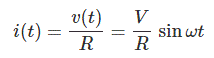
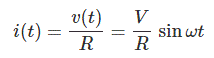
De esa expresión se puede concluir que la corriente tiene la misma fase con el voltaje aplicado.
Impedancia de un circuito RL en serie
Deduzcamos la expresión de la impedancia de un circuito RL en serie. Aquí la resistencia del valor R y inductancia del valor L están conectados en serie. El valor de la reactancia del inductor es L. Por lo tanto, la expresión de la impedancia en forma compleja es
El valor numérico o valor mod de la reactancia es
![]()
![]()
Impedancia de un circuito RC en serie
Conectemos una resistencia de valor R ohmio en serie con un condensador de capacitancia C farad. La reactancia del condensador es 1 / C. La resistencia R y la reactancia del condensador están en serie la expresión de la impedancia se puede escribir como
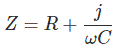
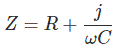
El valor mod de la impedancia del circuito RC en serie es
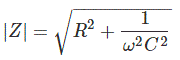
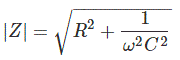
Impedancia de un circuito RL paralelo
Aquí la resistencia y inductores están conectados en paralelo. Aquí la reciprocidad de la impedancia del circuito es la suma de la reciprocidad de la resistencia y la reciprocidad de la reactancia.
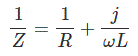
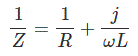
La expresión de la impedancia de la circuito RL paralelo puede representarse como
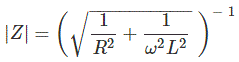
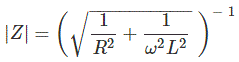
Impedancia de un circuito RC paralelo
Aquí como el condensador y resistencia están conectados en paralelo, el recíproco de la impedancia del circuito es la suma del recíproco de la resistencia y el recíproco de la reactancia del condensador.
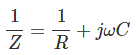
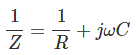
Finalmente, podemos escribir la expresión de la impedancia del circuito RC paralelo como
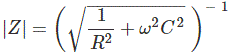
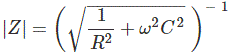
Impedancia de un circuito RLC en serie
Aquí resistencias…los condensadores e inductores están conectados en serie. La reactancia total del circuito es la suma de la reactancia de los inductores y condensadores. La reactancia de los condensadores se toma como negativa. La expresión de la impedancia de un circuito RLC en serie es
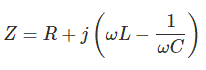
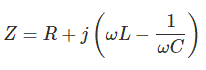
Impedancia de un circuito RLC paralelo
Aquí resistencia…el condensador y el inductor están conectados en paralelo. De la misma manera, la impedancia equivalente de un circuito RLC paralelo puede determinarse y la expresión final de la impedancia de un circuito RLC paralelo es
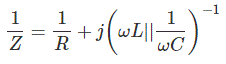
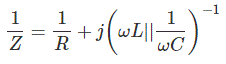
Representación polar de la impedancia