Este puente nos proporciona el método más adecuado para comparar los dos valores de condensador si descuidamos las pérdidas dieléctricas en el circuito del puente. El circuito de El puente de Sautys se muestra a continuación.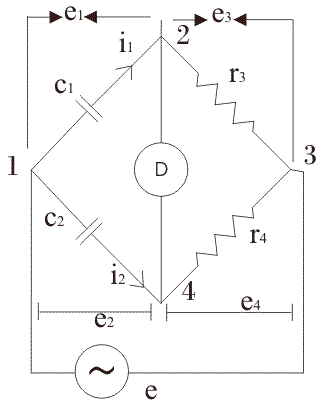

Batería se aplica entre los terminales marcados como 1 y 4. El brazo 1-2 consiste en el condensador c1 (cuyo valor se desconoce) que lleva actual i1 como se muestra, el brazo 2-4 consiste en puro resistencia (aquí resistencia pura significa que asumimos que no es de naturaleza inductiva), el brazo 3-4 también consiste en resistencia pura y el brazo 4-1 consiste en un condensador estándar cuyo valor ya conocemos.
Derivemos la expresión para el condensador c1 en términos de condensadores y resistencias estándar.
En la condición de equilibrio que tenemos,![]()
![]()
Implica que el valor del condensador está dado por la expresión![]()
![]()
Para obtener el punto de equilibrio debemos ajustar los valores de cualquiera de los dos r3 o r4 sin perturbar ningún otro elemento del puente. Este es el método más eficiente de comparar los dos valores del condensador si todas las pérdidas dieléctricas se descuidan del circuito.
Ahora dibujemos y estudiemos el diagrama de fáseres de este puente. El diagrama fásico de El puente de Sauty se muestra a continuación: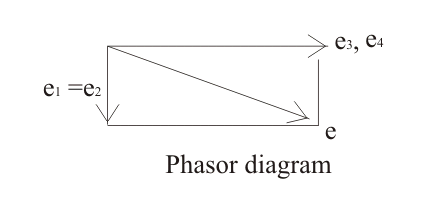

Marquemos el actual caída a través de un condensador desconocido como e1, Caída de tensión a través de la resistencia.3 be e3…caída de voltaje a través del brazo 3-4 be e…4 y la caída de voltaje a través del brazo 4-1 be e2. En la condición de equilibrio, la corriente fluye por el camino 2-4 será cero y también las caídas de tensión e1 y e3 ser igual a las caídas de voltaje e2 y e4 respectivamente.
Para dibujar el diagrama de fases hemos tomado e3 (o e4) eje de referencia, e1 y e2 se muestran en ángulo recto con e1 (o e2). ¿Por qué están en ángulo recto el uno con el otro? La respuesta a esta pregunta es muy simple ya que el condensador está conectado allí, por lo tanto el ángulo de diferencia de fase obtenido es de 90o.
Ahora bien, en lugar de algunas ventajas como que el puente es bastante simple y proporciona cálculos fáciles, hay algunas desventajas de este puente porque este puente da resultados inexactos para condensadores imperfectos (aquí imperfecto significa condensadores que no están libres de pérdidas dieléctricas). Por lo tanto, podemos utilizar este puente sólo para comparar condensadores perfectos.
Aquí estamos interesados en modificar el El puente de Sautys…queremos tener un puente que nos dé resultados precisos también para los condensadores imperfectos. Esta modificación está hecha por Grover. El diagrama de circuito modificado se muestra a continuación: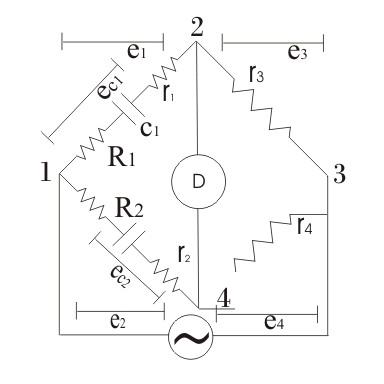

Aquí Grover ha presentado resistencias eléctricas r1 y r2 como se muestra arriba en los brazos 1-2 y 4-1 respectivamente, para incluir las pérdidas dieléctricas. También ha conectado las resistencias R1 y R2 respectivamente en los brazos 1-2 y 4-1. Derivemos el condensador de expresión c1 cuyo valor es desconocido para nosotros. De nuevo conectamos el condensador estándar en el mismo brazo 1-4 como hemos hecho en El puente de Sautys. En el punto de equilibrio al igualar las caídas de voltaje que tenemos:![]()
![]()
Al resolver la ecuación anterior obtenemos:![]()
![]()
Esta es la ecuación requerida.
Haciendo el diagrama de fáseres podemos calcular el factor de disipación. El diagrama de fases para el circuito anterior se muestra a continuación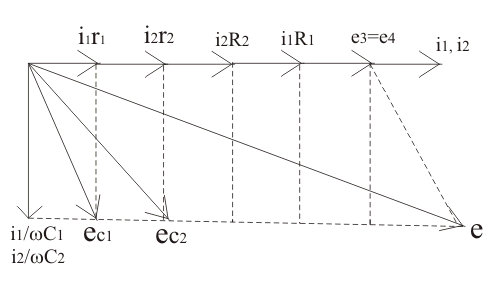

Vamos a marcar…1 y2 ser ángulos de fase de los condensadores c1 y c2 condensadores respectivamente. Del diagrama de fases tenemos tan(1) = factor de disipación = c1r1 y de manera similar tenemos el bronceado.2) = c2r2.
De la ecuación (1) tenemos

al multiplicar ambos lados tenemos

![]()
![]()
Por lo tanto, la expresión final para el factor de disipación se escribe como![]()
![]()
Por lo tanto, si se conoce el factor de disipación de un condensador. Sin embargo, este método da resultados bastante inexactos para el factor de disipación.