Contenido
- ¿Qué es el filtro activo?
- ¿Qué es el filtro activo de paso bajo?
- Filtro de paso bajo activo de primera orden
- Filtro activo de paso bajo de primer orden con amplificación
- Configuración invertida del filtro de paso bajo activo de primer orden
- Filtro de paso bajo activo de primer orden Configuración no invertida
- Ganancia de tensión del filtro de paso bajo de primer orden
- Función de transferencia de filtros de paso bajo activos de primera orden
- Diseño y ejemplo de un filtro activo de paso bajo de primer orden
- Circuito de filtro activo de paso bajo
- Curva de respuesta de frecuencia del filtro de paso bajo activo
- Filtro de amplificador no inversor
- Invertir el filtro del amplificador
- Filtro de paso bajo activo de segunda orden
- Ganancia de voltaje del filtro de paso bajo activo de segundo orden
- Frecuencia de corte del filtro de paso bajo activo de segundo orden
- Diseño y ejemplo de un filtro activo de paso bajo de segundo orden
- Aplicaciones del filtro activo de paso bajo
- Filtrado activo en aplicaciones de audio para automóviles
- Filtros activos de paso bajo para aplicaciones biomédicas
¿Qué es el filtro activo?
El filtro activo es un tipo de filtro que incluye uno o más componentes del circuito activo como un transistor o amplificador operacional (Op-Amp). Derivan su energía de una fuente externa de energía y la usan para aumentar o amplificar la salida de la señal.
También se pueden utilizar amplificadores operacionales para formar o cambiar la respuesta de frecuencia del circuito haciendo que el ancho de banda de salida de los filtros sea más estrecho o incluso más amplio, generando una reacción de salida más selectiva. Un Op-Amp tiene una alta impedancia de entrada, una baja impedancia de salida y una ganancia de voltaje dentro de su bucle de retroalimentación que surge de la mezcla de la resistencia. Los filtros activos, cuando se usan con un cuidadoso diseño de circuito, generan excelentes características de rendimiento, muy buena precisión con un rodaje pronunciado y poco ruido.
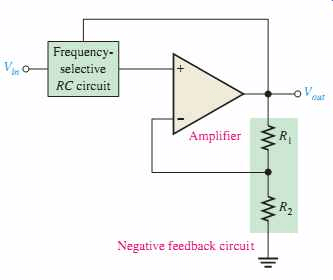

¿Qué es el filtro activo de paso bajo?
Si un filtro activo sólo permite componentes de baja frecuencia y niega todos los demás componentes de alta frecuencia, entonces se denomina Filtro de paso bajo activo (lo opuesto a un filtro de paso alto). Los filtros activos de paso bajo están compuestos por Op-Amp. La entrada del Op-Amp son señales de alta impedancia, que producen una señal de baja impedancia como salida.
El rendimiento del amplificador es un factor muy importante a la hora de diseñar un filtro activo de paso bajo. Hay dos tipos principales de filtros activos de paso bajo, a saber, el tipo de condensador conmutado y el tipo de condensador continuo. Los filtros están disponibles desde el primer orden hasta el octavo orden de diseño.
La respuesta de frecuencia de los circuitos será la misma que la del filtro RC pasivo, excepto que la banda pasante voltaje La ganancia aumenta la amplitud de la señal de salida. La banda de paso comienza desde 0Hz o DC para un filtro de paso bajo y continúa en -3dB hasta el punto de corte designado. Las señales son atenuadas más allá de la frecuencia de corte. Los filtros de paso bajo activos se agrupan según el orden del filtro. Discutiremos 1st & 2y ordenar filtros activos de paso bajo.
Filtro de paso bajo activo de primera orden
A filtro activo de paso bajo de primer orden es un filtro simplista que se compone de un solo componente reactivo Capacitor que acompaña a un componente activo Op-Amp. Se utiliza una resistencia con el condensador o inductor para formar el filtro de paso bajo RC o RL respectivamente. En un circuito pasivo, la amplitud de la señal de salida es menor que la amplitud de la señal de entrada. Para superar este problema, se introdujeron diseños de circuitos activos. Cuando un filtro pasivo de paso bajo se conecta a un Op-Amp, ya sea en invertir o no invertido da un diseño de filtro activo de paso bajo. La conexión de un simple circuito RC con un solo Op-Amp se muestra en la imagen de abajo.
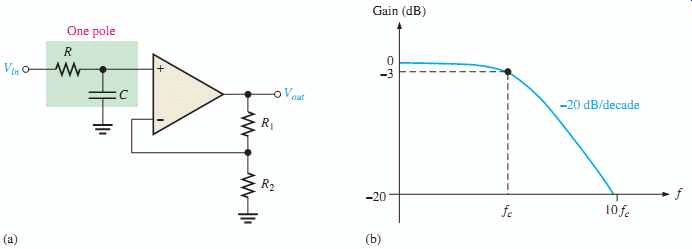

Este circuito RC ayuda a proporcionar una señal de baja frecuencia a la entrada del amplificador. El amplificador funciona como un circuito de búfer de salida de ganancia unitaria. Este circuito tiene una entrada añadida impedancia valor. El Op-Amp del circuito tiene un valor de impedancia de salida muy bajo, lo que ayuda a proporcionar una alta estabilidad al filtro.
Cuando se compara con el filtro pasivo, un filtro activo tiene una disposición en la que el amplificador está diseñado como un seguidor de voltaje (Buffer) que da una ganancia de DC de uno. Esta configuración proporciona una excelente estabilidad al filtro y tiene una alta ganancia de potencia. El principal inconveniente de este filtro es que no tiene ganancia de voltaje por encima de uno, que puede ser rectificado con un diseño de circuito extra.
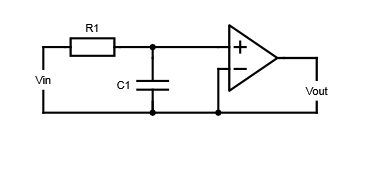

Filtro activo de paso bajo de primer orden con amplificación
Como ya se ha dicho, el diseño del filtro anterior no proporciona una ganancia de voltaje superior a uno. Por lo tanto, necesitamos modificar el circuito como se muestra a continuación.
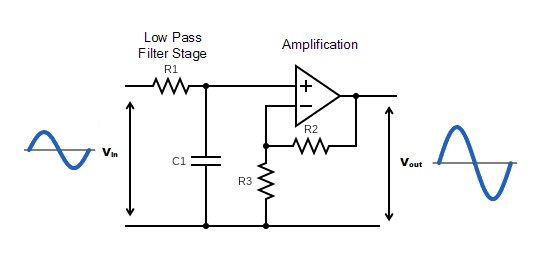

A frecuencias más bajas, las señales de entrada fluyen directamente a través del circuito amplificador. Cuando la frecuencia de la frecuencia de entrada aumenta, es desviada y se hace pasar por el condensador C. Esto aumenta la amplitud de la señal de salida por la ganancia de la banda de paso.
En una configuración de circuito de amplificador no inversor, la medición de la ganancia de tensión para el filtro se da como una relación de la resistencia de retroalimentación ( R2 ) dividido por su correspondiente resistencia de entrada ( R3 ) valor.


Configuración invertida del filtro de paso bajo activo de primer orden
El filtro inverso de paso bajo está diseñado usando el IC741, un Op-Amp con una configuración de 8 pines. En el modo de inversión, la salida del Op-Amp está 180 grados fuera de fase con la señal de entrada. Inicialmente, el Op-Amp tiene que ser alimentado con corriente continua. La cantidad de energía de CC dependerá de cuán grande sea la señal que se amplifique en la salida. La salida es una señal de CA que tiene un valor de pico. En este ejemplo, vamos a diseñar el circuito para una ganancia de 10, por lo que el voltaje de suministro de 12VDC se suministra a V+el pin 7 del Op-Amp y el -12VDC se suministra a V– el pin 4 del Op-Amp. Esto se denomina configuración Op-Amp invertida y la señal de salida será invertida que la de entrada.
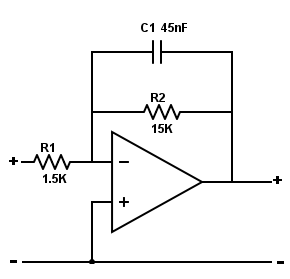

Filtro de paso bajo activo de primer orden Configuración no invertida
En esta configuración también se utiliza el IC741 Op-Amp. Pero, aquí la señal de entrada y la de salida estarán en fase entre sí. El RC que forma la parte del filtro de paso bajo es la primera mitad del circuito. Luego la señal pasa a través del Op-Amp, donde la señal es amplificada por una ganancia de voltaje que es proporcional a las resistencias R2 y R1. En esta configuración la impedancia externa no tiene ningún efecto sobre la reactancia del condensador, así la estabilidad mejoró.
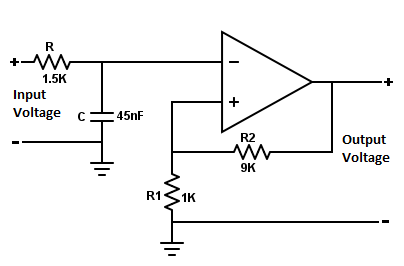

Ganancia de tensión del filtro de paso bajo de primer orden
Los componentes de frecuencia se utilizan para obtener la ganancia de voltaje del filtro.
![]()
![]()
donde,
Ven es el voltaje de entrada
Vfuera es el voltaje de salida
Af es la ganancia de banda pasante del filtro (1+R2/R1)
f es la frecuencia de la señal de entrada en Hertz
fc es la frecuencia de corte en Hertz
Cuando se aumenta la frecuencia, entonces la ganancia se reduce en 20 dB. El funcionamiento de un filtro de paso bajo activo puede comprobarse a partir de la ecuación anterior de ganancia de frecuencia. Sea f la frecuencia de funcionamiento y fc ser la frecuencia de corte.
A baja frecuencia
![]()
![]()
Cuando la frecuencia de funcionamiento es igual a la frecuencia de corte
![]()
![]()
Y a alta frecuencia
![]()
![]()
A partir de las ecuaciones anteriores, se ve que a bajas frecuencias la ganancia del circuito es igual al valor máximo de la ganancia. Mientras que a altas frecuencias la ganancia del circuito es mucho menor que la ganancia máxima de Af. Cuando la frecuencia de funcionamiento es igual a la frecuencia de corte, la ganancia es igual a 0,707 Af. En estos circuitos de filtro, el valor cuantitativo (magnitud) de la ganancia de la banda pasante se expresa en decibeles o dB que es una función de la ganancia de voltaje.


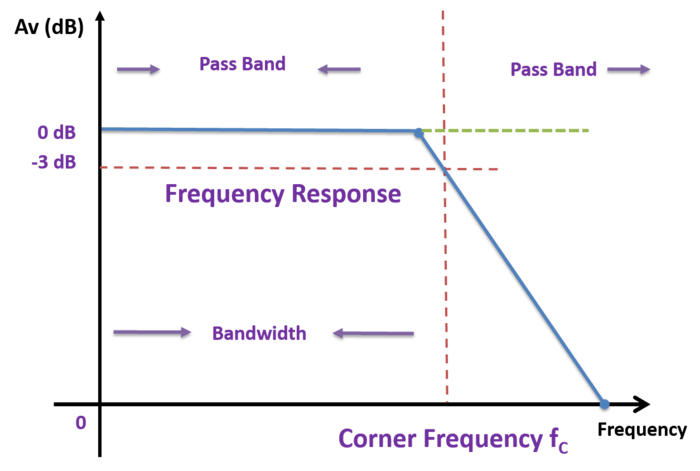

Función de transferencia de filtros de paso bajo activos de primera orden
El función de transferencia también se conoce como función de sistemas o función de red de la sistema de control. Se expresa como una función matemática. Cuando se usa en el análisis del dominio de frecuencia de un sistema, utiliza métodos de transformación como la transformación de Laplace. Los filtros trabajan en la frecuencia de la señal.
Así pues, las descripciones analíticas y gráficas que utilizan el dominio de la frecuencia son los instrumentos más potentes para describir la conducta de los filtros. Así, se utilizan comúnmente las ecuaciones del dominio de la frecuencia y las curvas de ganancia frente a la frecuencia y de fase frente a la frecuencia. Se requiere su descripción matemática en términos de la función de transferencia de sistemas para estudiar el dominio de la frecuencia de las redes. La función de transferencia de voltaje es la proporción de Laplace se transforma de las señales de salida y entrada para un esquema particular como se muestra a continuación.




Donde V0(s) y Vi(s) son los voltajes de salida y entrada y s es la compleja variable de transformación de Laplace.
Un filtro de paso bajo unipolar está diseñado para aplicaciones de baja frecuencia conectando una resistencia y un condensador como se muestra a continuación.
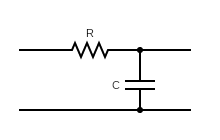

La función de transferencia del circuito anterior puede darse como


Ahora, en la ecuación anterior, las constantes laplace son reemplazadas por su valor equivalente en el dominio de la frecuencia.


El valor absoluto de la función de transferencia se define como magnitud o ganancia de voltios y puede representarse como se muestra a continuación


La frecuencia a la que la resistencia es igual a la impedancia del condensador, se dice que está a la frecuencia crítica que se da a continuación.
![]()
![]()
Por lo tanto,


Después de la sustitución adecuada en esta ecuación, obtenemos


El desplazamiento de fase del filtro viene dado por
![]()
![]()
La frecuencia de corte y el desplazamiento de fase del filtro pueden calcularse de la siguiente manera




Se puede obtener una configuración de filtro similar para el orden n-ésimo, cuando las etapas RC se unen en cascada.
Diseño y ejemplo de un filtro activo de paso bajo de primer orden
Diseñe un circuito de filtro de paso bajo activo no inversor que tenga una ganancia de diez a bajas frecuencias, un corte de alta frecuencia o frecuencia de esquina de 175Hz y una impedancia de entrada de 20K.
La ganancia de voltaje del amplificador no inversor se da como


Ahora supongamos que el valor de R1 es 1K y calculamos el valor R2 de la ecuación anterior.


Por lo tanto, para una ganancia de voltaje de 10, los valores de R1 y R2 son 1K y 9K respectivamente. La ganancia en dB se da como 20LogA = 20Log10 = 20dB
Ahora se nos da el valor de la frecuencia de corte como 175Hz y el valor de la impedancia de entrada como 20K. Sustituyendo estos valores en la ecuación y el valor de C puede calcularse como sigue.



 = 45.47nF
= 45.47nF
Así pues, a continuación se muestra el diseño final del filtro y su curva de respuesta en frecuencia equivalente.
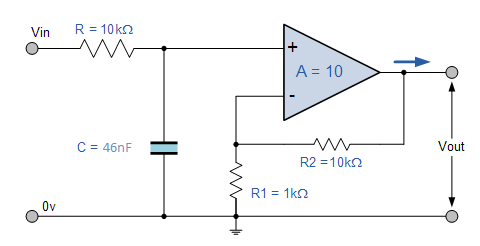
Circuito de filtro activo de paso bajo
A continuación se muestra un circuito típico para un filtro activo de paso bajo:

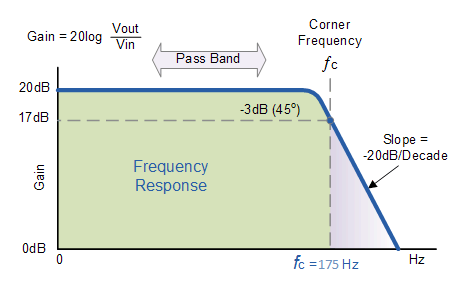
Curva de respuesta de frecuencia del filtro de paso bajo activo
A continuación se muestra la curva de respuesta de frecuencia para un filtro de paso bajo activo:

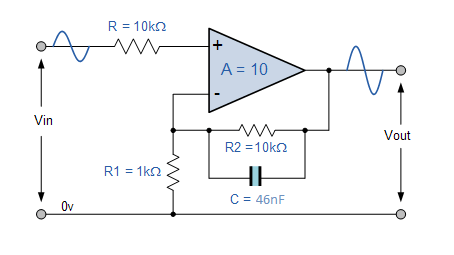
Filtro de amplificador no inversor
A continuación se presenta un simple filtro amplificador no inversor:

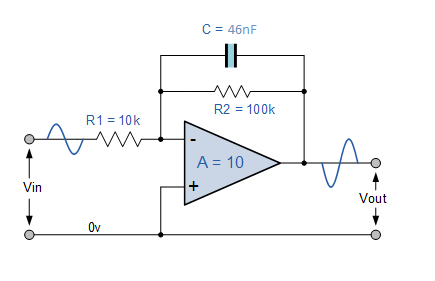
Invertir el filtro del amplificador
A continuación se presenta un filtro de amplificador inversor equivalente:

Filtro de paso bajo activo de segunda orden
Los filtros de segundo orden también se atribuyen como filtros VCVS ya que el Op-Amp utilizado aquí es un amplificador de fuente de voltaje controlado. Este es otro tipo importante de filtro activo usado en aplicaciones. La respuesta en frecuencia del filtro de paso bajo de segundo orden es indistinguible de la del tipo de primer orden, además de que el roll-off de la banda de parada será el doble que el de los filtros de primer orden a 40dB/década. Por consiguiente, los pasos de diseño deseados del filtro pasabajos activo de segundo orden son idénticos. Un método simple para obtener un filtro de segundo orden es poner en cascada dos filtros de primer orden.
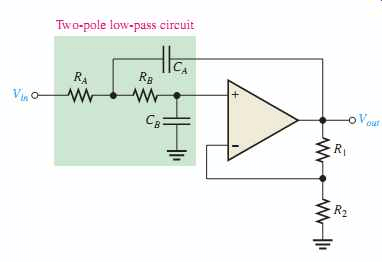

Cuando los circuitos de los filtros se conectan en cascada a los filtros de orden superior, la ganancia total de los filtros es igual al producto de cada etapa. Los filtros activos de segundo orden (bipolares) son esenciales porque pueden utilizarse para diseñar filtros de orden superior. Los filtros con un valor de orden pueden construirse poniendo en cascada filtros de primer y segundo orden.
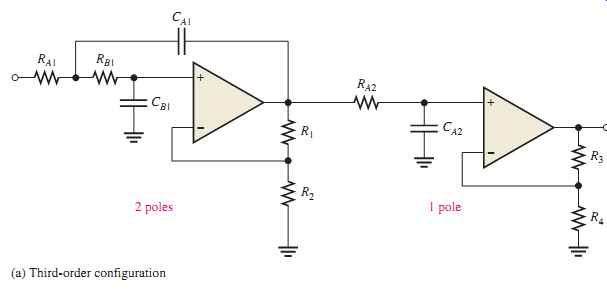

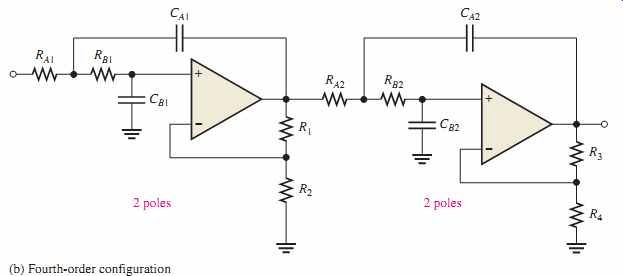

Ganancia de voltaje del filtro de paso bajo activo de segundo orden
La ganancia del filtro de segundo orden es un producto de la ganancia de n etapas que se suceden en cascada. Por ejemplo, si dos filtros de primer orden se ponen en cascada, la ganancia del filtro será la siguiente.




Si la ganancia de ambas etapas se da en dB, entonces la ganancia total se calcula sumando ambas ganancias


Frecuencia de corte del filtro de paso bajo activo de segundo orden
La ecuación de frecuencia de corte se da como
![]()
![]()
Cuando R3 = R4 = R y C1 = C2 = C, entonces la frecuencia de corte se dará como


La ganancia en la frecuencia de corte de la primera etapa del filtro es de -3dB. Para el filtro de segundo orden, combinando la ganancia de dos filtros de primer orden, la ganancia total será de -6dB.
Diseño y ejemplo de un filtro activo de paso bajo de segundo orden
Supongamos que Rs1 = Rs2 = 15K y el condensador C1 = C2 = 100nF. Las resistencias de ganancia son R1=1K, R2= 9K, R3 = 6K, y R4 =3K. Diseñe un filtro activo de paso bajo de segundo orden con estas especificaciones.
La frecuencia de corte se da como
![]()
![]()
(1) ![]()
![]()


La ganancia del amplificador de primera etapa es


![]()
![]()


La ganancia del amplificador de segunda etapa es


![]()
![]()


Ganancia total del filtro




La ganancia total en dB
(2) 

(3) 

La ganancia en la frecuencia de corte es
(4) 

Aplicaciones del filtro activo de paso bajo
Estos filtros se usan predominantemente en aplicaciones electrónicas como en altavoces y subwoofers. Actúan como filtro en los altavoces y como entradas para los subwoofers. También juegan un papel importante en el diseño de amplificadores y ecualizadores de audio. Cuando se utilizan convertidores analógicos a digitales, estos filtros se utilizan como filtros antialiasing para controlar las señales. Cuando se trata de la acústica y el sonido, el filtro se utiliza para impedir que las señales de alta frecuencia transmitan sonido para evitar los ecos.
Filtrado activo en aplicaciones de audio para automóviles
Los amplificadores operacionales son uno de los bloques de construcción más populares de los circuitos de audio de los automóviles. Para aumentar la eficiencia del audio, muchos desarrolladores eligen integrar amplificadores operacionales en sus circuitos de audio automotriz. Los filtros activos eliminan la posibilidad de interferencias no deseadas en la señal de audio. El filtrado es esencial para ayudar a asegurar un sonido de alta calidad para el sistema de audio de un automóvil. Un filtro con un Op-Amp o filtro activo, mientras amplifica la señal de audio, retiene la respuesta de frecuencia. Otro uso popular de los filtros Op-Amp en un sistema de audio automotriz es distinguir los rangos de frecuencia en todo el vehículo para los altavoces individuales. Sin embargo, la energía necesaria para accionar un gran subwoofer, particularmente a mayores volúmenes, podría dañar un altavoz de mayor frecuencia. Se puede utilizar HPF y LPF para establecer las frecuencias de corte para proporcionar frecuencias a los altavoces adecuados.
Filtros activos de paso bajo para aplicaciones biomédicas
Para el bajo voltaje y la baja energía, Sistema de monitorización de ECG aplicaciones, se utiliza un LPF CMOS activo con topología de amplificador operacional de dos etapas. Este amplificador de dos etapas compensado por Miller se puede utilizar en aplicaciones de CMRR de baja potencia y alto voltaje como herramientas biomédicas y pequeños dispositivos que funcionan con baterías como un marcapasos cardíaco, electrocardiograma (ECG) donde el bajo consumo de energía es la principal preocupación.