La ley Wiedemann-Franz es la ley que relaciona la conductividad térmica () y el conductividad eléctrica () de un material que consiste en electrones que se mueven libremente en él.
- Conductividad térmica (): Es el grado (medida) de capacidad de un material para conducir el calor.
- Conductividad eléctrica (): Es el grado (medida) de capacidad de un material para conducir electricidad.
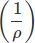
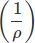
En los metales; cuando la temperatura aumenta, la velocidad de los electrones libres aumenta y eso lleva a un aumento de la transferencia de calor y también aumenta las colisiones entre los iones de la red y los electrones libres. Esto resulta en la caída de la conductividad eléctrica.
La ley define la relación entre el papel electrónico de la conductividad térmica de un material y la conductividad eléctrica de un material (metal) es directamente relativa a la temperatura.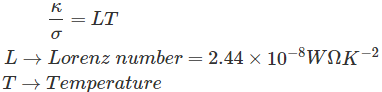
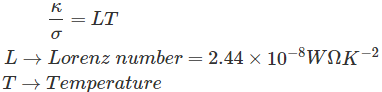
Esta ley se llama así por Gustav Wiedemann y Rudolph Franz en 1853 informó que la proporción 
Derivación de la Ley
Para ello, tenemos que asumir un material isotrópico homogéneo. Este material se somete entonces a un gradiente de temperatura 
El calor que fluye a través del material por unidad de tiempo por unidad de área es el flujo de calor. Será proporcional al gradiente de temperatura.![]()
![]()
K Coeficiente de conductividad térmica (W/mK)
K = Kphonon + Kelectróndesde la transferencia de calor en los sólidos debido al fonón y al electrón.
Ahora, podemos derivar la expresión para el coeficiente de conductividad térmica.
Para ello, tenemos que asumir que el flujo de calor es de temperatura más alta a temperatura más baja en una losa de metal que tiene un gradiente de temperatura de 
![]()
![]()
cv Calor específico
n Número de partículas por unidad de volumen
significa camino libre de colisiones
v velocidad de los electrones
Comparando las ecuaciones (1) y (2), obtenemos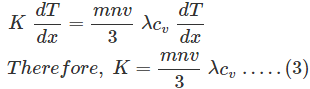
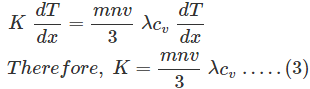
Sabemos que la energía de los electrones libres es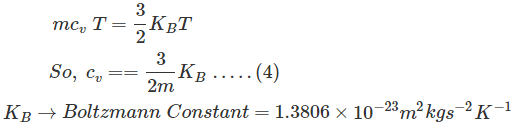
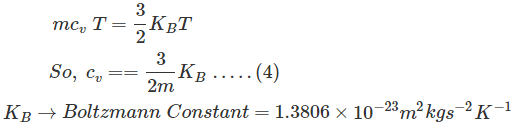
Ponemos la ecuación (4) en (3)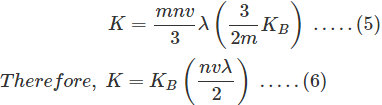
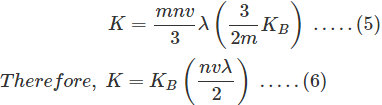
Ahora, el calor específico para un gas ideal a volumen constante,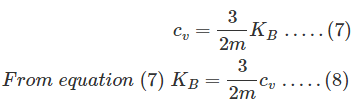
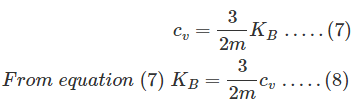
Cuando ponemos la ecuación (8) en (6), obtenemos![]()
![]()
A continuación, podemos considerar la densidad de corriente eléctrica de un metal con la aplicación de campo eléctrico, E (figura 1)
J = E ; Ley de Ohms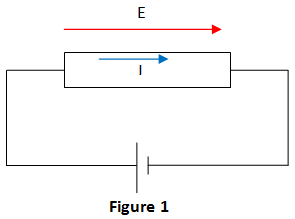

![]()
![]()
Así que, la forma correcta de La ley de Ohms está dada por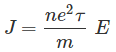
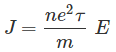
Hay un camino libre medio y un tiempo medio entre las colisiones.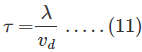
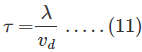
e Carga del electrón = 1.602 10-9 C
Tiempo de colisión o tiempo medio: Es el tiempo promedio para que el electrón se mueva o viaje antes de la dispersión.
vd → Velocidad de deriva: Es la velocidad estándar del electrón durante el tiempo de colisión.
Cuando ponemos la ecuación (11) en (10), obtenemos la conductividad eléctrica (Conductividad Drude) como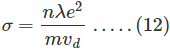
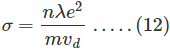
Considere los electrones que se mueven en un metal sin ninguna aplicación de campo eléctrico. Entonces el teorema de la equiparación viene dado por![]()
![]()
De la ecuación (13) obtenemos m como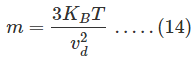
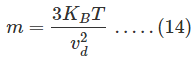
Ahora, ponemos la ecuación (14) en (12)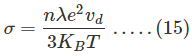
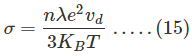
Así, obtuvimos los valores de K y de la ecuación (6) y (15).
Ahora, podemos tomar la proporción 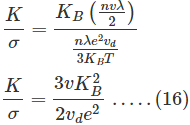
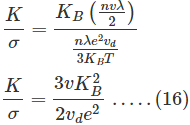
Asumimos que v = vdentonces la ecuación (16) se convierte en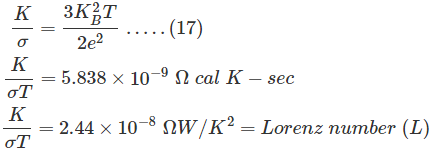
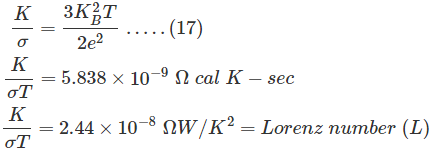
A partir de esto, podemos decir que la proporción 
Limitaciones de la Ley Wiedemann Franz
- El valor de L no es el mismo para todos los materiales.
- Esta ley no es válida para la temperatura intermedia.
- En los metales puros, ambos y aumenta a medida que la temperatura disminuye.