El sistema numérico con el que estamos más familiarizados es un sistema numérico decimal. El sistema numérico decimal tiene una base de diez, lo que implica que hay diez números con cuya ayuda podemos representar cualquier número de la familia decimal. Los números van del 0 al 9. La representación es como (15)10 la base 10 se escribe como sufijo o radix. Si no se escribe, entonces por defecto debemos entender que es un número decimal por defecto.
Por otro lado, el número binario inventado por Gottfried Leibniz en 1679 tiene una base de dos. Bi significa dos, así que a partir de ahí podemos decir que la base del sistema binario es 2. Es decir, sólo dos números son suficientes para representar un número en formato binario. Los números que se usan en el sistema numérico binario son el 0 y el 1.
El número binario puede ser representado poniendo 2 en el prefijo que denota la base. Si no se indica la base, se supone por defecto que es un número decimal. Hay que tener mucho cuidado al escribir un número binario, un pequeño error puede resultar en un error muy grave. Por ejemplo, un número binario se escribe de la siguiente manera-
(00110)2.
Ahora puede surgir una pregunta, ¿por qué necesitamos un número binario? Tenemos un sistema de números decimales que nos es familiar y la mayoría de las personas no entienden el binario. La respuesta es que cualquier dispositivo programable o un procesador puede trabajar en dos modos, alto o bajo. Aquí, alto denota que el suministro está conectado a ese punto y bajo denota que el punto está conectado a tierra o está en un estado de cero voltios. Esto se llama lógica positiva y en otro sistema lógico se toma lo contrario, lo que se conoce como sistema de lógica negativa.
Además, podemos decir que un alto significa que realiza alguna función o trabajo y un bajo indica que no ha realizado ningún trabajo. Lo contrario también puede ser cierto si tomamos el sistema de lógica negativa. Así, de la descripción anterior podemos decir que es mucho más fácil y conveniente de usar sistema numérico binario en la computadora en lugar de decimal y también se requerirá la conversión para que el resultado de salida que se da en forma binaria se convierta en decimal por el bien del usuario.
Conversión de Binario a Decimal
Conversión de números enteros
Expande el número dado en forma binaria en la potencia de 2 y suma los valores, el resultado que obtendremos será en forma decimal. Por ejemplo…
Convertir un número binario en un número decimal
Conversión del número de puntos decimales a decimales
Esto también se puede hacer de la misma manera, sin embargo después del punto decimal el número debe ser multiplicado por 2-1, 2-2 etc.
Por ejemplo,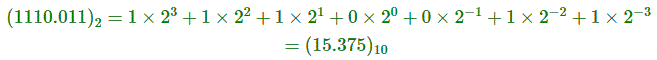
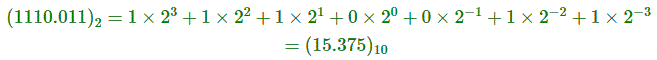
Conversión de decimal a binario
Números enteros
Dividir el número por 2 y tomar sólo el resto, si la división se completa que tomar sólo el resto que da el número binario.
Ejemplo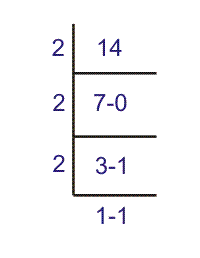

Así pues, el equivalente binario del (14)10 es (1110)2
Después del guión (-) se escribe el resto.
Supongamos que estamos convirtiendo el número decimal (87)10. Ahora la conversión se muestra a continuación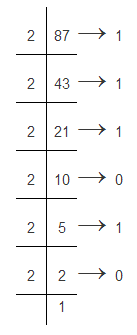
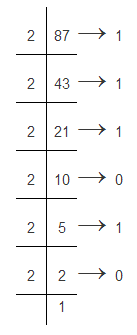
Para los números fraccionarios
En este caso, se hace la multiplicación sucesiva. El número que se quiere convertir se multiplica con la base o el radio del número binario que es 2. Se saca la parte entera o el acarreo del producto y se repite el mismo proceso hasta obtener un número entero. Por ejemplo…
El equivalente binario de (.95)10 se evalúa de la siguiente manera-

Dado que no obtenemos el valor entero después de multiplicaciones sucesivas, podemos aproximar el valor a ser (.111110.)2.
Conversión del número negativo
En caso de un número negativo podemos ir por 2s complemento la representación de un número firmado.
Ejemplo- 9 = 0000 1001
1s complemento = 1111 0110.
Sumando 1 obtenemos = 11110111 que es la representación del complemento 2s de (-9).

