Matriz de incidencia es esa matriz que representa el gráfico de tal manera que con la ayuda de esa matriz podemos dibujar un gráfico. Esta matriz puede ser denotada como [AC] Como en todas las matrices, también hay filas y columnas en matriz de incidencia [AC].
Las filas de la matriz [AC] representan el número de nodos y la columna de la matriz [AC] representan el número de ramas en el gráfico dado. Si hay n número de filas en una matriz de incidencia dada, eso significa que en un gráfico hay n número de nodos. De manera similar, si hay m número de columnas en esa matriz de incidencia dada, eso significa que en ese gráfico hay m número de ramas.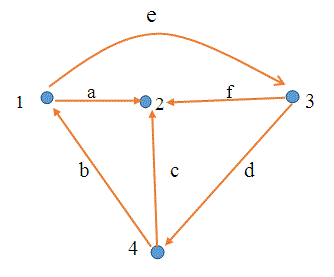

En el gráfico anterior o gráfico dirigido, hay 4 nodos y 6 ramas. Por lo tanto, el matriz de incidencia para el gráfico anterior tendrá 4 filas y 6 columnas.
Las entradas de la matriz de incidencia son siempre -1, 0, +1. Esta matriz es siempre análoga a KCL (Ley actual de Krichoff). Por lo tanto, de la KCL podemos derivar eso,
| Tipo de rama | Valor |
| La rama saliente de kth nodo | +1 |
| La rama entrante a kth nodo | -1 |
| Otros | 0 |
Pasos para construir la matriz de incidencia
A continuación, los pasos para dibujar la matriz de incidencia :-
- Si un determinado kth El nodo tiene una rama saliente, entonces escribiremos +1.
- Si un determinado kth El nodo tiene una rama entrante, entonces escribiremos -1.
- El resto de las ramas se considerarán 0.
Ejemplos de Matriz de Incidencia


Para el gráfico mostrado arriba escriba su matriz de incidencia.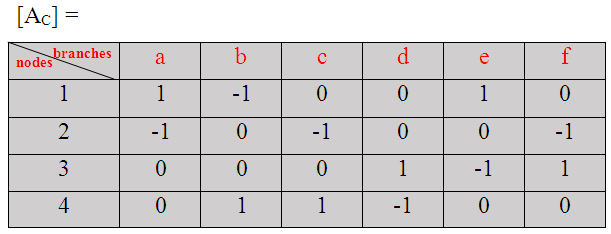

Matriz de incidencia reducida
Si de un determinado matriz de incidencia [AC], cualquier fila arbitraria es eliminada, entonces la nueva matriz formada será una matriz de incidencia reducida. Está representada por el símbolo [A]. El orden de la matriz de incidencia reducida es (n-1) b donde n es el número de nodos y b es el número de ramas.
Para el gráfico anterior, la matriz de incidencia reducida será…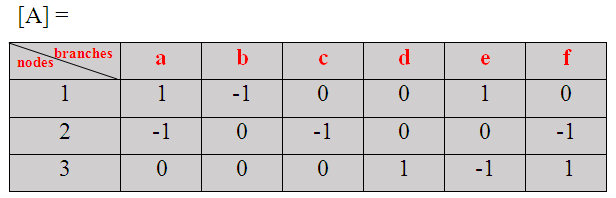

[NOTA :- En la matriz mostrada arriba se borra la fila 4.]
Ahora consideremos un nuevo ejemplo relacionado con la matriz de incidencia reducida. Para el gráfico mostrado arriba escriba su matriz de incidencia reducida.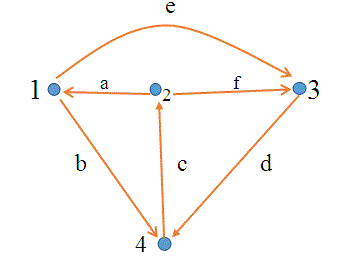

Respuesta:- Para dibujar la matriz de incidencia reducida, primero dibuje su matriz de incidencia. Su matriz de incidencia es…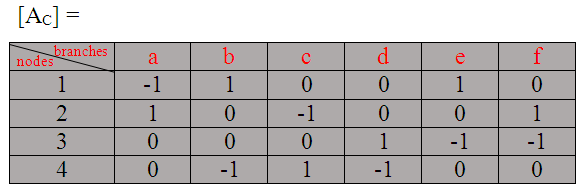

Ahora dibujando su matriz de incidencia reducida. Para ello sólo tenemos que eliminar cualquier nodo (en esto hemos eliminado el nodo 2). Su matriz de incidencia reducida es:-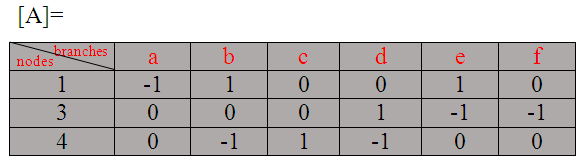

Esta es la respuesta requerida.
Puntos para recordar
- Para comprobar la corrección de la matriz de incidencia que hemos dibujado, debemos comprobar la suma de la columna.
- Si la suma de la columna llega a ser cero, entonces la matriz de incidencia que hemos creado es correcta, si no, incorrecta.
- La matriz de incidencia puede aplicarse sólo a la gráfica dirigida.
- El número de entradas en una fila aparte de cero nos dice el número de ramas vinculadas a ese nodo. Esto también se llama grado de ese nodo.
- El rango de completo matriz de incidencia es (n-1), donde n es el número de nodos del gráfico.
- La matriz de orden de incidencia es (n b), donde b es el número de ramas del gráfico.
- De una determinada reducción matriz de incidencia podemos dibujar completos matriz de incidencia simplemente añadiendo +1, 0 o -1 con la condición de que la suma de cada columna sea cero.