Sistema de números de complemento
La palabra complemento en el sistema numérico significa la diferencia del número con el número más alto de ese dígito. Esta definición puede aplicarse a varios sistemas numéricos y también se denominan de forma diferente. Pero en general, si un número tiene una base de N, entonces eso se conoce como complemento de (N-1). Sin embargo, si añadimos uno con ese valor que nos dará Ns complemento. Por ejemplo, empecemos con un número decimal porque estamos familiarizados con ese sistema numérico. Tomemos un número 25. El complemento se puede averiguar de dos maneras y como tiene una base de 10, que se llamará como (10 1) que es Complemento de los 9s.
Método 1: El primer método es restar el número del número más alto de ese dígito, lo que implica que el número tiene que ser restado del 99. Así que obtenemos (99 25) que es 74.
Método 2: En el segundo método cada dígito se considera individualmente y se resta de 9 ya que 9 es el más alto. Así que obtenemos 9 2, 9 5, lo que significa que la respuesta es 74. Así que tenemos la misma respuesta y ambos métodos de encontrar el complemento es verdadero y puede ser aplicado de acuerdo a nuestra voluntad.
Sistema numérico binario: Ahora llegando a un número binario que es nuestro principal tema de discusión. Tiene sólo dos dígitos 0 y 1 y por lo tanto el nombre es binario. Tiene una base de 2, así que si lo restamos del número más alto de ese dígito entonces obtenemos (2 1) que es 1s complemento. Si se añade 1 con eso, entonces tendremos un complemento de 2s. Además, si se resta el dígito individual de 1 (el más alto entre 0 y 1) entonces también obtendremos un complemento de 1s y si se suma uno con eso nos dará 2s complemento. Sin embargo, por suerte para nosotros hay otro método para encontrar el complemento 1s. No tenemos que recordar todos esos pasos para encontrar el complemento 1 y 2, pero un simple truco hará el trabajo.
Dos métodos son similares que hemos discutido anteriormente pero un nuevo método o truco que podemos usar para encontrar el complemento 1s. Rompamos el suspenso y veamos las diversas metodologías para encontrar 1s y 2s complemento con un ejemplo. Por ejemplo, tenemos que averiguar 2s complemento de 0100. Aquí, se ha usado un cero antes del número para que sea un número de cuatro bits. Ya que, tenemos un número de bits en el poder de dos para un sistema binario.
Método 1 En este método tenemos que restarlo del 1111 ya que es el número de cuatro dígitos más alto para averiguar 1s complemento. 1111 0100 es 1011. El complemento de 2s será 1011 + 1 que es 1100.
Método 2 Aquí, resta cada dígito individual de 1 para obtener 1s complemento. Cuyo resultado será 1 0, 1 1, 1 0, 1 0, 1 0 que es 1011.
2s complemento será 1011 + 1 = 1100.
Método 3 Aquí, sólo tenemos que reemplazar 1 por 0 y 0 por 1 para saber el complemento de 1s. Sumando uno con ese resultado nos dará un complemento de 2s.
Para el 0100, tendremos un complemento de 1s con sólo reemplazar 1 por 0 y 0 por 1 y esto dará el resultado 1011. Sumando 1 con ese resultado nos dará (1011 + 1) que es 1100.
Así que en los tres métodos vemos que hemos encontrado el mismo resultado y todos los métodos son correctos y uno puede usar cualquiera de ellos según su conveniencia.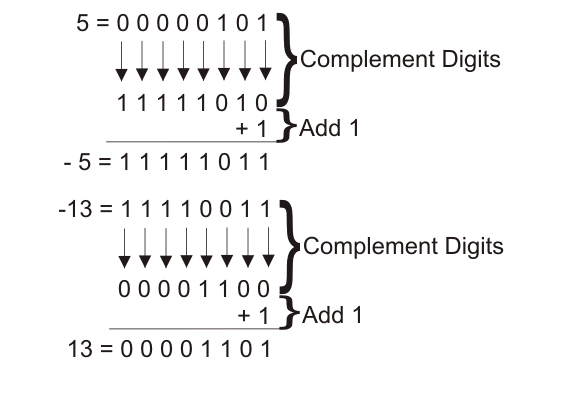

2s complementan la representación de los números positivos y negativos.
¿Por qué necesitamos un complemento de dos?
El principal problema de la utilización de 2s complemento es que se puede utilizar para la sustracción de dos dígitos binarios. El ordenador sólo entiende binario como sabemos, y no hay nada llamado como número negativo en el sistema numérico binario pero es absolutamente necesario representar un número negativo utilizando el binario, lo que puede hacerse asignando un bit de signo al número que es un bit extra requerido. Si el bit de signo es 1, entonces el número se considera negativo y si es 0, entonces el número se llamará positivo.
Para la sustracción de números binarios que se puede hacer de la siguiente manera-
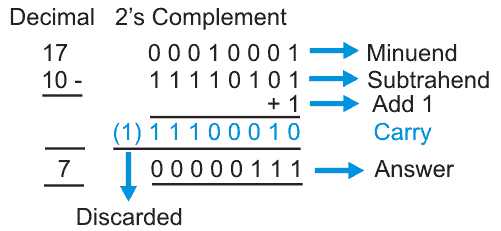
Restar un número menor de un número mayor
- Encuentra 2s complemento del número menor.
- Sume el mayor y el complemento de 2s del número menor.
- Descarte el equipaje.
- Después de descartar la carga, guarda el resultado que será la respuesta a la sustracción.

Restar el número más grande del número más pequeño
- Encuentra 2s complemento de un número mayor.
- Añade 2s de complemento del número mayor al número menor.
- Si no se genera ningún arrastre, encuentre el complemento de 2s del resultado y el resultado será negativo.
- Si se genera una carga, descarte la carga y tome el resultado que será la respuesta y el signo será negativo.


Sustracción de un número mayor a un número menor.
Ventajas del complemento 2s
- La sustracción puede hacerse con la ayuda del método del complemento 2s.
- Es fácil de lograr con un circuito más grande.
- No es necesario que se lleve a cabo la carga final como en el caso de 1s complemento.
- El número negativo puede representarse utilizando 2s complemento.